题目内容
20.解答题:(1)已知a+b=5,ab=3,求a-b的值
(2)解方程:$\frac{x}{x-1}-1=\frac{3}{(x-1)(x+2)}$.
分析 (1)先根据题意得出的值,再根据完全平方公式把(a-b)2展开并代入数据求出其值,然后根据平方根的定义求解即可;
(2)先去分母,把分式方程化为整式方程求出x的值,再代入最减公分母进行检验即可.
解答 解:(1)∵a+b=5,ab=3,
∴(a+b)2=25,即a2+b2+2ab=25,
∴a2+b2=25-6=19,
∴(a-b)2=a2+b2-2ab,
=19-2×3,
=13,
即a-b=±$\sqrt{13}$;
(2)原式可化为x(x+2)-(x-1)(x+2)=3,
整理得,x+2=3,解得x=1,
当x=1时,(x-1)(x+2)=0,
故x=0是原分式方程的增根,即原分式方程无解.
点评 本题考查的是完全平方公式,熟记完全平方公式是解答此题的关键.

练习册系列答案
相关题目
5.若(m-2)x|2m-3|=6是一元一次方程,则m的值为( )
| A. | 2 | B. | 2或1 | C. | 1 | D. | 不能确定 |
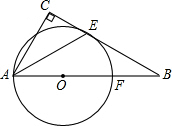 如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是30°.
如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是30°.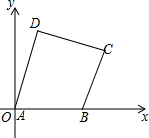 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)