题目内容
11.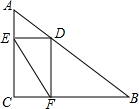 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )| A. | 5 | B. | 4.8 | C. | 4.6 | D. | 4.4 |
分析 连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.
解答 解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,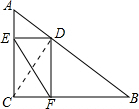
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵DE⊥AC,DF⊥BC,∠C=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•CD,
即$\frac{1}{2}$×8×6=$\frac{1}{2}$×10•CD,
解得CD=4.8,
∴EF=4.8.
故选B.
点评 本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
16.下列关于实数a说法正确的是( )
| A. | a的相反数是-a | B. | a的倒数是-a | C. | a的绝对值是±a | D. | a的平方是正数 |
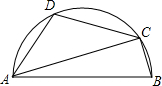 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.