题目内容
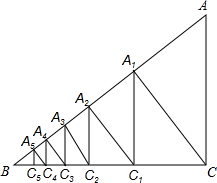 如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=
如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=| CnAn+1 |
| AnCn |
考点:相似三角形的判定与性质
专题:规律型
分析:由Rt△ABC中,AC=3,BC=4,可求得AB的长,然后由CA1⊥AB,利用三角形的面积可得,直角三角形斜边上的高等于直角边相乘除以斜边,即可求得CA1的长,然后由三角形函数的性质,求得
(其中n为正整数)的值.
| CnAn+1 |
| AnCn |
解答:解:∵Rt△ABC中,AC=3,BC=4,
∴AB=
=5,
∵CA1⊥AB,
∴CA1=
=
,cos∠B=
=
,
∵A1C1⊥BC,
∴∠CA1B=∠A1C1B=90°,
∴∠CA1C1+∠A1CB=∠B+∠A1CB=90°,
∴∠CA1C1=∠B,
同理:∠AnCnAn+1=∠B,
∴cos∠AnCnAn+1=
=
.
故答案为:
,
.
∴AB=
| AC2+BC2 |
∵CA1⊥AB,
∴CA1=
| AC•BC |
| AB |
| 12 |
| 5 |
| AC |
| AB |
| 4 |
| 5 |
∵A1C1⊥BC,
∴∠CA1B=∠A1C1B=90°,
∴∠CA1C1+∠A1CB=∠B+∠A1CB=90°,
∴∠CA1C1=∠B,
同理:∠AnCnAn+1=∠B,
∴cos∠AnCnAn+1=
| CnAn+1 |
| AnCn |
| 4 |
| 5 |
故答案为:
| 12 |
| 5 |
| 4 |
| 5 |
点评:此题考查了直角三角形的性质以及三角函数等知识.此题难度适中,注意得到∠AnCnAn+1=∠B是解此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
下列计算正确的是( )
| A、2m+3n=5mn | ||||||
| B、(x2)3=x5 | ||||||
| C、(a-b)2=a2-b2 | ||||||
D、
|
 如图,在?ABCD中,CD=3,AD=5,AE平分交∠BAD边于点E,则线段BE,CE的长分别是( )
如图,在?ABCD中,CD=3,AD=5,AE平分交∠BAD边于点E,则线段BE,CE的长分别是( )| A、2和3 | B、3和2 |
| C、4和1 | D、1和4 |
 如图,正方形ABCD内接于⊙O,它的边长为4cm,则⊙O的半径是( )
如图,正方形ABCD内接于⊙O,它的边长为4cm,则⊙O的半径是( )A、2
| ||
B、4
| ||
| C、2cm | ||
| D、4cm |
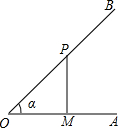 如图,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值为
如图,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值为 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=4cm,则OE的长为
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=4cm,则OE的长为