题目内容
论a取什么实数,点P(a-1,3-2a)都在直线l上,Q(m,n)是直线l上的点,则(2m+n-2)2的值等于 .
考点:一次函数图象上点的坐标特征
专题:
分析:先令a=0,则P(-1,3);再令a=1,则P(0,1),由于a不论为何值此点均在直线l上,设此直线的解析式为y=kx+b(k≠0),把两点代入即可得出其解析式,再把Q(m,n)代入即可得出2m-n的值,进而可得出结论.
解答:解:∵令a=0,则P(-1,3);再令a=1,则P(0,1),由于a不论为何值此点均在直线l上,
∴设此直线的解析式为y=kx+b(k≠0),
∴
,
解得
,
∴此直线的解析式为:y=-2x+1,
∵Q(m,n)是直线l上的点,
∴-2m+1=n,即2m+n=1,
∴原式=(1-2)2=1.
故答案为:1.
∴设此直线的解析式为y=kx+b(k≠0),
∴
|
解得
|
∴此直线的解析式为:y=-2x+1,
∵Q(m,n)是直线l上的点,
∴-2m+1=n,即2m+n=1,
∴原式=(1-2)2=1.
故答案为:1.
点评:本题考查的是一次函数图象上点的坐标特点,即一次函数图象上点的坐标一定适合此函数的解析式.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
某市场道路改造中,需要铺设一条长为1200米的管道,为了尽量减少施工对交通造成的影响,实际施工时,工作效率比原计划提高了25%,结果提前了8天完成任务,设原计划每天铺设管道x米,根据题意列出方程为 .
看表,则相应的代数式是( )
| x | 0 | 1 | 2 | 3 |
| 代数式值 | 2 | -1 | -4 | -7 |
| A、x+2 | B、2x-3 |
| C、3x-1 | D、-3x+2 |
下列方程中,是关于x的一元二次方程的是( )
A、x2+
| ||
| B、ax2+bx+c=0 | ||
| C、(x-1)(x+2)=0 | ||
| D、3x2+4xy-y2=0 |
如果2是一元二次方程x2+kx+2=0的一个根,那么常数k的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
 如图,点P在抛物线y=(x-2)2+1上,设点P的坐标为(x,y),当0≤x≤3时,y的取值范围为
如图,点P在抛物线y=(x-2)2+1上,设点P的坐标为(x,y),当0≤x≤3时,y的取值范围为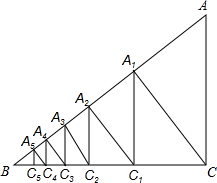 如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=
如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=