题目内容
 如图,正方形ABCD内接于⊙O,它的边长为4cm,则⊙O的半径是( )
如图,正方形ABCD内接于⊙O,它的边长为4cm,则⊙O的半径是( )A、2
| ||
B、4
| ||
| C、2cm | ||
| D、4cm |
考点:正多边形和圆
专题:
分析:作OE⊥AD于E,连接OD,在Rt△ADE中,根据垂径定理和勾股定理即可求解.
解答: 解:作OE⊥AD于E,连接OD,则AE=DE=2cm,OE=2cm.
解:作OE⊥AD于E,连接OD,则AE=DE=2cm,OE=2cm.
在Rt△ADE中,OD=
=2
(cm).
故选:A.
 解:作OE⊥AD于E,连接OD,则AE=DE=2cm,OE=2cm.
解:作OE⊥AD于E,连接OD,则AE=DE=2cm,OE=2cm.在Rt△ADE中,OD=
| ED2+OE2 |
| 2 |
故选:A.
点评:此题主要考查了正多边形和圆,本题需仔细分析图形,利用勾股定理即可解决问题.

练习册系列答案
相关题目
如果2是一元二次方程x2+kx+2=0的一个根,那么常数k的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
若代数式
有意义,则实数x的取值范围是( )
| ||
| x+1 |
| A、x≠-1 | B、x≥0 |
| C、x>0 | D、x≤0且x≠-1 |
下列说法正确的是( )
| A、无理数就是开方开不尽的数 |
| B、无理数是无限不循环小数 |
| C、带根号的数都是无理数 |
| D、无限小数都是无理数 |
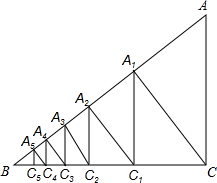 如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=
如图.已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=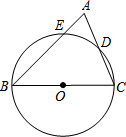 如图,BC为⊙O的直径,AB交⊙O于E点,AC交⊙O于D点,AD=CD,∠A=70°,现给出以下四个结论:
如图,BC为⊙O的直径,AB交⊙O于E点,AC交⊙O于D点,AD=CD,∠A=70°,现给出以下四个结论: