题目内容
热气球的探测器显示，从热气球看一栋高楼顶部的俯角为60°，看这栋高楼底部的俯角为80°，若这栋高楼有82.6m，问热气球与高楼的水平距离是多少？（结果精确到0.1米）
【答案】分析：延长BA交PD与D．在Rt△APD中，利用∠APD的正切函数求出邻边AD的长；进而可在Rt△BPD中，利用已知角的三角函数求出BD的长；由AB=BD-AD即可求出楼的高度．
解答：
解：延长BA交PD与D．
∵tan60°=
，∴DA=tan60°•PD，
∵tan80°=
，∴DB=tan80°•PD，
∴tan80°•PD-tan60°•PD=82.6，
PD=
≈21.0（米）．
答：热气球与高楼的水平距离约是21.0米．
点评：本题考查俯角的定义，要求学生能借助俯角构造直角三角形并解直角三角形．
解答：
解：延长BA交PD与D．∵tan60°=
，∴DA=tan60°•PD，∵tan80°=
，∴DB=tan80°•PD，∴tan80°•PD-tan60°•PD=82.6，
PD=
≈21.0（米）．答：热气球与高楼的水平距离约是21.0米．
点评：本题考查俯角的定义，要求学生能借助俯角构造直角三角形并解直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
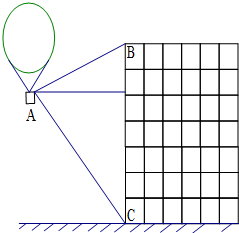21、热气球的探测器显示，从热气球上看一栋高楼顶部的仰角为28°，看这栋高楼底部的俯角为62°，热气球与高楼之间的水平距离为66m，这栋高楼有多高？（结果精确到0.1m，参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53，sin62°≈0.88，cos62°≈0.47，tan62°≈1.88）
如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°．热气球A的高度为240米，求这栋大楼的高度．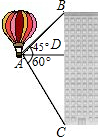
如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为50m，求这栋楼的高度．（
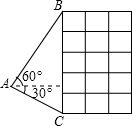如图热气球的探测器显示，从热气球上看一栋高楼顶部的仰角为60°，看这栋高楼底部的俯角为30°，若热气球与高楼水平距离为60m，则这栋楼的高度为
（2013•德阳）如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为60°，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为（ ）