Question

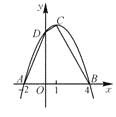
【题目】在平而直角坐标系中，已知点，直线经过点．抛物线恰好经过三点中的两点．

判断点是否在直线上．并说明理由；

求的值；

平移抛物线，使其顶点仍在直线上，求平移后所得抛物线与轴交点纵坐标的最大值．

Answer 1

【答案】（1）点在直线上，理由见详解；（2）a=-1，b=2；（3）

【解析】

（1）先将A代入，求出直线解析式，然后将将B代入看式子能否成立即可；

（2）先跟抛物线与直线AB都经过（0，1）点，且B，C两点的横坐标相同，判断出抛物线只能经过A，C两点，然后将A，C两点坐标代入得出关于a，b的二元一次方程组；

（3）设平移后所得抛物线的对应表达式为y=-（x-h）2+k，根据顶点在直线上，得出k=h+1，令x=0，得到平移后抛物线与y轴交点的纵坐标为-h2+h+1，在将式子配方即可求出最大值．

（1）点在直线上，理由如下：

将A（1，2）代入得，

解得m=1，

∴直线解析式为，

将B（2，3）代入，式子成立，

∴点在直线上；

（2）∵抛物线与直线AB都经过（0，1）点，且B，C两点的横坐标相同，

∴抛物线只能经过A，C两点，

将A，C两点坐标代入得，

解得：a=-1，b=2；

（3）设平移后所得抛物线的对应表达式为y=-（x-h）2+k，

∵顶点在直线上，

∴k=h+1，

令x=0，得到平移后抛物线与y轴交点的纵坐标为-h2+h+1，

∵-h2+h+1=-（h-）2+，

∴当h=时，此抛物线与轴交点的纵坐标取得最大值．