Question

【题目】抛物线y=﹣x2﹣x+与x轴交于点A，B（点A在点B的左边），与y轴交于点C，点D是该抛物线的顶点．

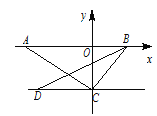
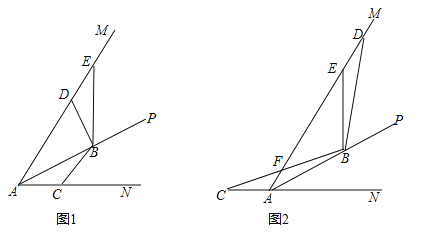
（1）如图1，连接CD，求线段CD的长；

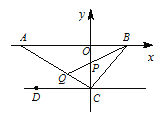
（2）如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；

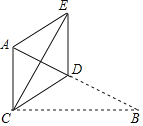
（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C的位置，再将△O2B2C绕点B2旋转一周在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）（3），O2M的长或或或．

【解析】

（1）分别表示C和D的坐标，利用勾股定理可得CD的长；

（2）令y=0，可求得A（-3，0），B（，0），利用待定系数法可计算直线AC的解析式为：y=x+，设E（x，x+），P（x，﹣x2﹣x+），表示PE的长，利用勾股定理计算AC的长，发现∠CAO=30°，得AE=2EF=x+2，计算PE+EC，利用配方法可得当PE+EC的值最大时，x=-2，此时P（-2，），确定要使四边形PO1B1C周长的最小，即PO1+B1C的值最小，将点P向右平移个单位长度得点P1（-，），连接P1B1，则PO1=P1B1，再作点P1关于x轴的对称点P2（-，-），可得结论；

（3）先确定对折后O2C落在AC上，△AMN是以MN为腰的等腰三角形存在四种情况：

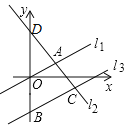
①如图4，AN=MN，证明△C1EC≌△B2O2M，可计算O2M的长；

②如图5，AM=MN，此时M与C重合，O2M=O2C=；

③如图6，AM=MN，N和H、C1重合，可得结论；

④如图7，AN=MN，过C1作C1E⊥AC于E证明四边形C1EO2B2是矩形，根据O2M=EO2+EM可得结论．

（1）如图1，过点D作DK⊥y轴于K，

当x=0时，y=，

∴C（0，），

y=﹣x2﹣x+=-，

∴D（-，），

∴DK=，CK=-=，

∴CD=；

（2）在y=-x2﹣x+中，令y=0，则-x2﹣x+=0，

解得：x1=-3，x2=，

∴A（-3，0），B（，0），

∵C（0，），

易得直线AC的解析式为：y=x+，

设E（x，x+），P（x，-x2﹣x+），

∴PF=-x2﹣x+，EF=x+，

Rt△ACO中，AO=3，OC=，

∴AC=2，

∴∠CAO=30°，

∴AE=2EF=x+，

∴PE+EC=（-x2﹣x+）-（x+）+（AC-AE），

=-x2-x+ [2-（x+）]，

=-x2-x-x，

=-（x+2）2+，

∴当PE+EC的值最大时，x=-2，此时P（-2，），

∴PC=2，

∵O1B1=OB=，

∴要使四边形PO1B1C周长的最小，即PO1+B1C的值最小，

如图2，将点P向右平移个单位长度得点P1（-，），连接P1B1，则PO1=P1B1，

再作点P1关于x轴的对称点P2（-，-），则P1B1=P2B1，

∴PO1+B1C=P2B1+B1C，

∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1，

∴B1（-，0），

将B1向左平移个单位长度即得点O1，

此时PO1+B1C=P2C=，

对应的点O1的坐标为（-，0），

∴四边形PO1B1C周长的最小值为；

（3）O2M的长度为或或2+或2-．

理由是：如图3，

∵H是AB的中点，

∴OH=，

∵OC=，

∴CH=BC=2，

∴∠HCO=∠BCO=30°，

∵∠ACO=60°，

∴将CO沿CH对折后落在直线AC上，即O2在AC上，

∴∠B2CA=∠CAB=30°，

∴B2C∥AB，

∴B2（-2，），

①如图4，AN=MN，

∴∠MAN=∠AMN=30°=∠O2B2O3，

由旋转得：∠CB2C1=∠O2B2O3=30°，B2C=B2C1，

∴∠B2CC1=∠B2C1C=75°，

过C1作C1E⊥B2C于E，

∵B2C=B2C1=2，

∴C1E＝=B2O2，B2E=，

∵∠O2MB2=∠B2MO3=75°=∠B2CC1，

∠B2O2M=∠C1EC=90°，

∴△C1EC≌△B2O2M，

∴O2M=CE=B2C-B2E=2-；

②如图5，AM=MN，此时M与C重合，O2M=O2C=，

③如图6，AM=MN，

∵B2C=B2C1=2=B2H，即N和H、C1重合，

∴∠CAO=∠AHM=∠MHO2=30°，

∴O2M=AO2=；

④如图7，AN=MN，过C1作C1E⊥AC于E，

∴∠NMA=∠NAM=30°，

∵∠O3C1B2=30°=∠O3MA，

∴C1B2∥AC，

∴∠C1B2O2=∠AO2B2=90°，

∵∠C1EC=90°，

∴四边形C1EO2B2是矩形，

∴EO2=C1B2=2，C1E＝B2O2＝，

∴EM=，

∴O2M=EO2+EM=2+，

综上所述，O2M的长是或或2+或2．