题目内容
1.等腰三角形的对称轴有( )| A. | 1条 | B. | 3条 | C. | 1条或3条 | D. | 无数条 |
分析 根据轴对称图形的概念进行求解即可.
解答 解:当等腰三角形是非等边三角形时,对称轴有1条;
当等腰三角形是等边三角形时,对称轴有三条.
故选C.
点评 本题考查了轴对称图形的知识,.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.

练习册系列答案
相关题目
11.化简|x-5|-|2x-13|(5<x<6)得( )
| A. | -x+8 | B. | 3x-18 | C. | -3x+18 | D. | x-8 |
13.下面关于函数的三种表示方法叙述错误的是( )
| A. | 用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化 | |
| B. | 用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值 | |
| C. | 用公式法表示函数关系,可以方便地计算函数值 | |
| D. | 任何函数关系都可以用上述三种方法来表示 |
10.如图:在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2015为止,则AP2015=( )
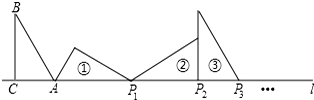

| A. | 2015+672$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2013+672$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |