题目内容
如图，已知AD为∠ABC中BC上中线，P为BD上一点，过P作AD的平行线交AB于点Q，交AC延长线于R，证明：PQ+PR=2AD．考点：平行线分线段成比例
专题：证明题
分析：由平行可得到
=
，
=
，再结合D为中点，可得BD=CD，再利用比例的和可得到结论．
| QP |
| AD |
| BP |
| BD |
| RP |
| AD |
| PC |
| CD |
解答：证明：∵AD∥RP，
∴
=
，
=
，
∵BD=CD，
∴
+
=
+
=2，
∴PQ+PR=2AD．
∴
| QP |
| AD |
| BP |
| BD |
| RP |
| AD |
| PC |
| CD |
∵BD=CD，
∴
| QP |
| AD |
| RP |
| AD |
| BP |
| BD |
| PC |
| CD |
∴PQ+PR=2AD．
点评：本题主要考查平行线分线段成比例的性质，分清平行线分线段成比例中的对应线段是解题的关键．
练习册系列答案
相关题目
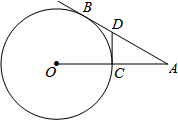如图，AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C的切线交AB于点D．若AD=2BD，CD=1，则⊙O的半径为