题目内容
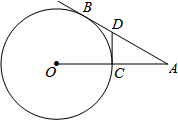 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=1,则⊙O的半径为
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=1,则⊙O的半径为考点:切线的性质
专题:
分析:连接OB,则可知DC=BD=1,则AD=2,在△ACD中可求得AC=
,设半径为r,则AO=r+
,在Rt△AOB中由勾股定理可得OA2=OB2+AB2,代入求r即可.
| 3 |
| 3 |
解答: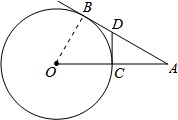 解:连接OB,
解:连接OB,
∵AB、CD都是⊙O的切线,
∴∠OBA=90°,且DC=BD=1,
∴AD=2BD=2,
∴AB=2+1=3,
在Rt△ACD中,可求得AC=
,
设半径为r,则OA=r+
,
在Rt△ABO中,由勾股定理可得:OA2=OB2+AB2,
即(r+
)2=r2+32,解得r=
,
故答案为:
.
 解:连接OB,
解:连接OB,∵AB、CD都是⊙O的切线,
∴∠OBA=90°,且DC=BD=1,
∴AD=2BD=2,
∴AB=2+1=3,
在Rt△ACD中,可求得AC=
| 3 |
设半径为r,则OA=r+
| 3 |
在Rt△ABO中,由勾股定理可得:OA2=OB2+AB2,
即(r+
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查切线的性质,掌握连接圆心和切点是常用的辅助线是解题的关键,注意方程思想的应用.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
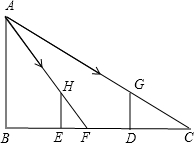 如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.
如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.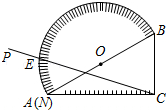 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是 如图,已知AD为∠ABC中BC上中线,P为BD上一点,过P作AD的平行线交AB于点Q,交AC延长线于R,证明:PQ+PR=2AD.
如图,已知AD为∠ABC中BC上中线,P为BD上一点,过P作AD的平行线交AB于点Q,交AC延长线于R,证明:PQ+PR=2AD. 如图所示,两条直线l1,l2的交点坐标可以看作方程组
如图所示,两条直线l1,l2的交点坐标可以看作方程组