题目内容
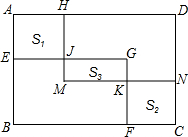如图，在矩形ABCD中，矩形EBFG通过平移变换得到矩形HMND，点E，F，N，H都在矩形ABCD的边上，若正方形AEJH和正方形CFKN的面积分别为S1，S2，矩形MKGJ的面积为S3．已知BE=3，BF=4，4S3=S1+S2，则S1+S2+S3=考点：矩形的性质,平移的性质
专题：
分析：设两个正方形的边长为x，表示出MK、JM，然后根据三个面积的关系列出方程并求出x，再分别求出S1、S2、S3，然后相加计算即可得解．
解答：解：设两个正方形的边长为x，则MK=BF-EJ=4-x，JM=BE-KF=3-x，
∵4S3=S1+S2，
∴4（4-x）（3-x）=2x2，
整理得，x2-14x+24=0，
解得x1=2，x2=12（舍去），
∴S1=S2=22=4，
S3=
（S1+S2）=
×（4+4）=2，
∴S1+S2+S3=4+4+2=10．
故答案为：10．
∵4S3=S1+S2，
∴4（4-x）（3-x）=2x2，
整理得，x2-14x+24=0，
解得x1=2，x2=12（舍去），
∴S1=S2=22=4，
S3=
| 1 |
| 4 |
| 1 |
| 4 |
∴S1+S2+S3=4+4+2=10．
故答案为：10．
点评：本题考查了矩形的性质，平移的性质，平移前后的两个图形能够完全重合，关键在于表示出MK、JM并列出方程．
练习册系列答案
相关题目
有理数a、b在数轴上的位置如图所示，化简|a-b|-|b-a|的结果是（ ）| A、2a+2b | B、2b |
| C、0 | D、2a |
乘积是1的两个数互为（ ）
| A、倒数 | B、相反数 |
| C、绝对值 | D、有理数 |
如图，正方形ABCD的边长为a，以直线AB为轴将正方形旋转一周，所得圆柱的主视图的周长为
在平面直角坐标系xOy中，将抛物线y=