题目内容
 如图,在⊙O中,半径OA⊥OB,弦AD与OB相交于点E,过点D的切线与OB的延长线相较于点C,且DE=DC,试探索∠A的大小,并证明你的结论.
如图,在⊙O中,半径OA⊥OB,弦AD与OB相交于点E,过点D的切线与OB的延长线相较于点C,且DE=DC,试探索∠A的大小,并证明你的结论.考点:切线的性质
专题:
分析:由半径OA⊥OB,过点D的切线与OB的延长线相较于点C,易证得∠AEO=∠DEC=∠EDC,即可证得EC=DC,又由DE=DC,可证得△DEC是等边三角形,继而求得答案.
解答:解:∠A=30°.
理由:∵半径OA⊥OB,
∴∠A+∠AEO=90°,
∵OA=OD,
∴∠A=∠ADO,
∵DC是⊙O的切线,
∴OD⊥DC,
∴∠ADO+∠EDC=90°,
∵∠AEO=∠DEC,
∴∠DEC=∠EDC,
∴EC=DC,
∵DE=DC,
∴EC=DE=DC,
即△CDE是等边三角形,
∴∠AEO=∠DEC=60°,
∴∠A=90°-∠AEO=30°.
理由:∵半径OA⊥OB,
∴∠A+∠AEO=90°,
∵OA=OD,
∴∠A=∠ADO,
∵DC是⊙O的切线,
∴OD⊥DC,
∴∠ADO+∠EDC=90°,
∵∠AEO=∠DEC,
∴∠DEC=∠EDC,
∴EC=DC,
∵DE=DC,
∴EC=DE=DC,
即△CDE是等边三角形,
∴∠AEO=∠DEC=60°,
∴∠A=90°-∠AEO=30°.
点评:此题考查了切线的性质、直角三角形的性质以及等边三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
在1,2,-2这三个数中,任意两数之商的最小值是( )
A、
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
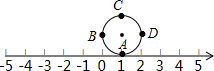 如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向左滚动.那么数轴上的-2014所对应的点将与圆周上字
如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向左滚动.那么数轴上的-2014所对应的点将与圆周上字 如图,在Rt△ABC中,∠C=90°,按要求填空:
如图,在Rt△ABC中,∠C=90°,按要求填空: 如图,圆桌正上方的灯光发出的光照射到桌面后在地面上形成圆形,已知桌面的直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面上阴影部分的直径为
如图,圆桌正上方的灯光发出的光照射到桌面后在地面上形成圆形,已知桌面的直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面上阴影部分的直径为