题目内容
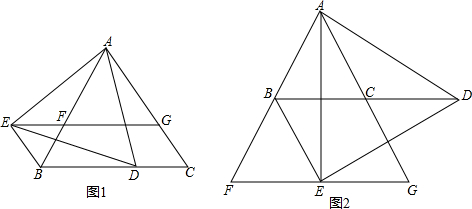
12. 如图,△ABC中,BD:DC=4:9,CE:EA=4:3,求AF:FB.
如图,△ABC中,BD:DC=4:9,CE:EA=4:3,求AF:FB.
分析 作DP∥AC交BE于P,DQ∥AB交FC于Q,根据平行线的性质得到PD:CE=BD:BC,DQ:BF=CD:BC,计算即可.
解答 解: 作DP∥AC交BE于P,DQ∥AB交FC于Q,
作DP∥AC交BE于P,DQ∥AB交FC于Q,
∵DP∥AC,
∴PD:CE=BD:BC=4:13,
∵CE:EA=4:3,
∴PD:EA=16:39,
∵DQ∥AB,
∴DQ:BF=CD:BC=9:13,
∴DQ:AF=OD:OA=16:39,
∴AF:BF=27:16.
点评 本题考查了平行线分线段成比例定理的应用,正确作出辅助线、能正确运用定理是解此题的关键.

练习册系列答案
相关题目
2.在如图的汽车标志图形中,是中心对称图形但不是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
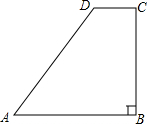 如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.
如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.