题目内容
6. 如图,商业大厦与电视台大厦的大楼顶部各有一个射灯,两条光柱的仰角(即光柱与水平面的夹角)∠2、∠3分别是60°、40°,则光柱相交时(在同一个平面内)的夹角∠1=80°.
如图,商业大厦与电视台大厦的大楼顶部各有一个射灯,两条光柱的仰角(即光柱与水平面的夹角)∠2、∠3分别是60°、40°,则光柱相交时(在同一个平面内)的夹角∠1=80°.
分析 过点A,作AB⊥BD,过点D作DC∥AB,利用平行线的性质和三角形的内角和定理即可求出∠1的度数.
解答 解:如图所示:
过点A,作AB⊥BD,过点D作DC∥AB,
∴∠4=∠2,
在△CDE中,∠1+∠3+∠4=180°,
∵∠2、∠3分别是60°、40°,
∴∠1=80°,
∴∠1=80°,
故答案为:80.
点评 本题考查了仰角的概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
6. 某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
频率分布统计表
请根据上述信息,解答下列问题:
(1)表中:a=15,b=0.35,c=0.1;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
 某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:频率分布统计表
| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.40 |
| 70≤x<80 | 35 | b |
| 80≤x<90 | a | 0.15 |
| 90≤x<100 | 10 | c |
(1)表中:a=15,b=0.35,c=0.1;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
11.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{{a^2}+3}$ | D. | $\sqrt{a{b^2}}$ |
18.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\frac{1}{{\sqrt{2}}}$ | C. | $\sqrt{2}$ | D. | $\sqrt{0.2}$ |
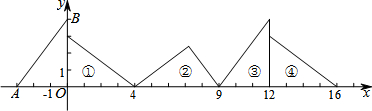
 如图所示,等腰三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),且AC=BC=5,反比例函数的图象经过点C.
如图所示,等腰三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),且AC=BC=5,反比例函数的图象经过点C. 将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是90°.
将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是90°.