题目内容
11.在△ABC中,若AB=AC=5,BC=8,则sinB=$\frac{3}{5}$.分析 根据勾股定理,可得AD的长,根据正弦函数等于对边比斜边,可得答案.
解答 解:作AD⊥BC于D,如图 ,
,
BD=$\frac{1}{2}$BC=4,
由勾股定理,得
AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3.
由正弦函数,得
sinB=$\frac{AD}{AB}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查了解直角三角形,利用勾股定理得出对边的长是解题关键,再利用正弦函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆.在看不见图形的情况下随机摸出1张,是中心对称图形的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.$\frac{1}{3}$的绝对值是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |

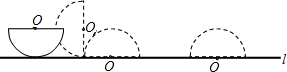
 如图,△ABC,用尺规作图作角平分线CD.(保留作图痕迹,不要求写作法)
如图,△ABC,用尺规作图作角平分线CD.(保留作图痕迹,不要求写作法)