��Ŀ����
����Ŀ�����������
�����ڷ������ijЩ��ѧ����ʱ������Ҫ�Ƚ������������ʽ�Ĵ�С�����������IJ���һ��Ҫ����һ����ת��,���С���������dz��õķ���֮һ����ν�������������ͨ��������Σ������ò�ķ�����ȷ�����ǵĴ�С��Ҫ�Ƚϴ���ʽ![]() ��
��![]() �Ĵ�С��ֻҪ�������ǵIJ�
�Ĵ�С��ֻҪ�������ǵIJ�![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��
��
��������
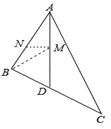
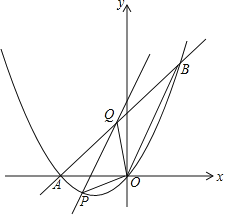
��ͼ���ԱȽ�ͼ�١�ͼ���������ε��ܳ�![]() ��
��![]() �Ĵ�С
�Ĵ�С![]() ��
��
��ͼ�εã�![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
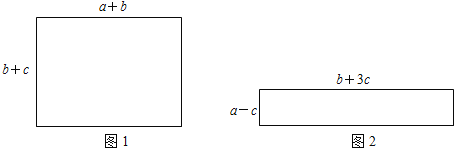
���Ӧ�ã�
��1���ò��Ͻ��ܵġ�������Ƚ�![]() ��
��![]() �Ĵ�С��
�Ĵ�С��
��ϵ��չ��
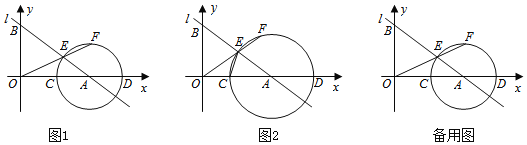
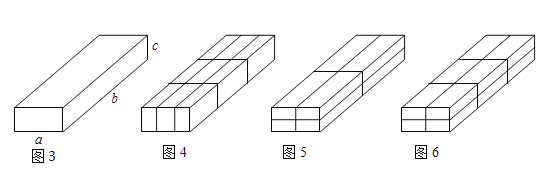
��2��С���ڳ���������һЩ��Ʒ����һ������������ӡ��������������ӵijߴ���ͼ3��ʾ������![]() �����ۻ�Ա�ֱ�ɰ�ͼ4��ͼ5��ͼ6���ַ����������������ַ���������̣����ַ������������˵�����ɣ�
�����ۻ�Ա�ֱ�ɰ�ͼ4��ͼ5��ͼ6���ַ����������������ַ���������̣����ַ������������˵�����ɣ�
���𰸡�(1)![]() ��(2) ͼ5�ķ���������̣�ͼ6�ķ��������
��(2) ͼ5�ķ���������̣�ͼ6�ķ��������
��������
(1)������������ʽ֮�����0�����������жϣ�
(2)�ֱ��ʾ��ͼ4����������ΪL1��ͼ5����������ΪL2��ͼ6����������ΪL3��������ʾ������֮��IJ���ɵó���С��ϵ��
(1)![]()
![]() (
(![]() )
)
![]()
![]() ��
��
��Ϊ![]() ��
��
����![]() ��
��
����![]() ��
��
(2)��ͼ4����������ΪL1����L1![]() ��
��
��ͼ5����������ΪL2����L2![]() ��
��
��ͼ6����������ΪL3����L3![]() ��
��
��L1-L2![]() ��
��
��L1��L2��
��L3-L2![]() ��
��
��L3-L1=![]() ��
��
��![]() ��
��
��![]() ��
��
��L3��L1��
��ڶ��ַ���������̣������ַ����������

 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�