Question

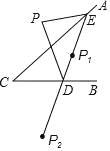
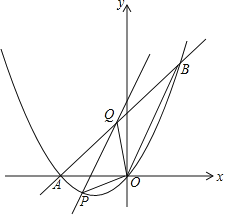
【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x=﹣2．

（1）求抛物线的解析式；

（2）设直线y=kx+4与抛物线两交点的横坐标分别为x1，x2（x1＜x2），当时，求k的值；

（3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ=1：2时，求出点P的坐标．

（坐标平面内两点M（x1，y1），N（x2，y2）之间的距离MN=）

Answer 1

【答案】（1）抛物线解析式为y=x2+x；（2）k=1；（3）P（﹣2，﹣2+2）．

【解析】（1）先利用对称轴公式得出b=4a，进而利用待定系数法即可得出结论；

（2）先利用根与系数的关系得出，x1+x2=4（k﹣1），x1x2=﹣16，转化已知条件，代入即可得出结论；

（3）先判断出OB=2PQ，进而判断出点C是OB中点，再求出AB解析式，判断出PC∥AB，即可得出PC解析式，和抛物线解析式联立解方程组即可得出结论．

（1）根据题意得，，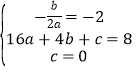

∴ ，

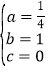∴抛物线解析式为y=x2+x；

（2）∵直线y=kx+4与抛物线两交点的横坐标分别为x1，x2，

∴x2+x=kx+4，

∴x2﹣4（k﹣1）x﹣16=0，

根据根与系数的关系得，x1+x2=4（k﹣1），x1x2=﹣16，

∵，

∴2（x1﹣x2）=x1x2，

∴4（x1﹣x2）2=（x1x2）2，

∴4[（x1+x2）2﹣4x1x2]=（x1x2）2，

∴4[16（k﹣1）2+64]=162，

∴k=1；

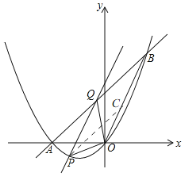
（3）如图，取OB的中点C，

∴BC=OB，

∵B（4，8），

∴C（2，4），

∵PQ∥OB，

∴点O到PQ的距离等于点O到OB的距离，

∵S△POQ：S△BOQ=1：2，

∴OB=2PQ，

∴PQ=BC，∵PQ∥OB，

∴四边形BCPQ是平行四边形，

∴PC∥AB，

∵抛物线的解析式为y=x2+x①，

令y=0，

∴x2+x=0，

∴x=0或x=﹣4，

∴A（﹣4，0），

∵B（4，8），

∴直线AB解析式为y=x+4，设直线PC的解析式为y=x+m，

∵C（2，4），

∴直线PC的解析式为y=x+2②，

联立①②解得，（舍）或，

∴P（﹣2，﹣2+2）．