题目内容
分解因式:
(1)4ma2-4mb2
(2)7(x2-y2)-6x(x-y)+16y2.
(1)4ma2-4mb2
(2)7(x2-y2)-6x(x-y)+16y2.
考点:提公因式法与公式法的综合运用
专题:计算题
分析:(1)原式提取公因式,再利用平方差公式分解即可;
(2)原式去括号整理后,利用完全平方公式分解即可.
(2)原式去括号整理后,利用完全平方公式分解即可.
解答:解:(1)原式=4m(a2-b2)=4m(a+b)(a-b);
(2)原式=7x2-7y2-6x2+6xy+16y2=x2+6xy+9y2=(x+3y)2.
(2)原式=7x2-7y2-6x2+6xy+16y2=x2+6xy+9y2=(x+3y)2.
点评:此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
将4x2-16因式分解,以下式子正确的是( )
| A、(2x-4)2 |
| B、(2x+8)(2x-8) |
| C、4(x+2)(x-2) |
| D、4(x-2)2 |
在△ABC和△A1B1C1中,已知∠A=∠A1,AB=A1B1,下列添加的条件中,不能判定△ABC≌△A1B1C1的是( )
| A、AC=A1C1 |
| B、∠C=∠C1 |
| C、BC=B1C1 |
| D、∠B=∠B1 |
9的算术平方根是( )
| A、3 | ||
| B、±3 | ||
| C、-3 | ||
D、
|
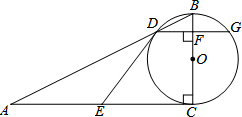 如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.
如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.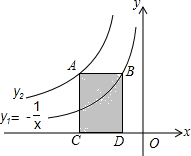 如图是双曲线y1、y2在第二象限的图象,其中y1=-
如图是双曲线y1、y2在第二象限的图象,其中y1=- △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.