题目内容
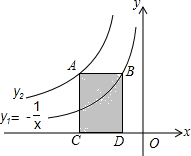 如图是双曲线y1、y2在第二象限的图象,其中y1=-
如图是双曲线y1、y2在第二象限的图象,其中y1=-| 1 |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:延长AB交y轴于E,如图,由于AC⊥x轴,BD⊥x轴,AB∥x轴,则根据反比例函数k的几何意义得到S矩形BDOE=1,于是有S矩形ACOE=3,所以|k|=3,然后去绝对值得到满足条件的k的值,从而得到双曲线y2的表达式.
解答:解:延长AB交y轴于E,如图,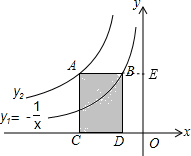
∵AC⊥x轴,BD⊥x轴,AB∥x轴,
∴S矩形BDOE=|-1|=1,
∴S矩形ACOE=2+1=3,
∴|k|=3,
而k<0,
∴k=-3,
∴双曲线y2的表达式为y=-
.
故答案为y=-
.

∵AC⊥x轴,BD⊥x轴,AB∥x轴,
∴S矩形BDOE=|-1|=1,
∴S矩形ACOE=2+1=3,
∴|k|=3,
而k<0,
∴k=-3,
∴双曲线y2的表达式为y=-
| 3 |
| x |
故答案为y=-
| 3 |
| x |
点评:本题考查了反比例函数系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
已知2y-x=2,则2x-4y的值为( )
| A、4 | B、-4 | C、8 | D、-8 |
比-1大的数是( )
| A、-3 | ||
| B、0 | ||
C、-
| ||
| D、-1 |
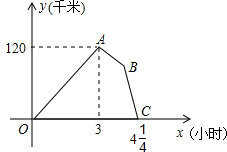 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )| A、快递车从甲地到乙地的速度为100千米/时 | ||
| B、甲、乙两地之间的距离为120千米 | ||
C、图中点B的坐标为(3
| ||
| D、快递车从乙地返回时的速度为90千米/时 |
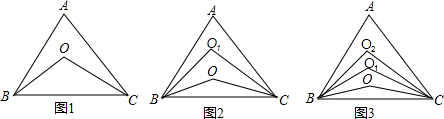
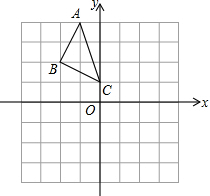 如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:
如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题: