题目内容
 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,△MNC≌△BAC,则∠BCN=( )
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,△MNC≌△BAC,则∠BCN=( )| A、10° | B、20° |
| C、50° | D、80° |
考点:全等三角形的性质
专题:
分析:根据比例设∠A=3k,∠ABC=5k,∠ACB=10k,然后利用三角形的内角和定理求出k,从而得到三个内角的度数,再根据全等三角形对应角相等求出∠M、∠N,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACN=∠M+∠N,然后根据∠BCN=∠ACB-∠ACN代入数据计算即可得解.
解答:解:设∠A=3k,∠ABC=5k,∠ACB=10k,
由三角形的内角和定理得,3k+5k+10k=180°,
解得k=10°,
所以,∠A=3×10°=30°,∠ABC=5×10°=50°,∠ACB=10×10°=100°,
∵△MNC≌△BAC,
∴∠M=∠ABC=50°,∠N=∠A=30°,
由三角形的外角性质得,∠ACN=∠M+∠N=50°+30°=80°,
∴∠BCN=∠ACB-∠ACN=100°-80°=20°.
故选B.
由三角形的内角和定理得,3k+5k+10k=180°,
解得k=10°,
所以,∠A=3×10°=30°,∠ABC=5×10°=50°,∠ACB=10×10°=100°,
∵△MNC≌△BAC,
∴∠M=∠ABC=50°,∠N=∠A=30°,
由三角形的外角性质得,∠ACN=∠M+∠N=50°+30°=80°,
∴∠BCN=∠ACB-∠ACN=100°-80°=20°.
故选B.
点评:本题考查了全等三角形对应角相等的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键,利用“设k法”求△ABC的三个内角更简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果在数轴上的A、B两点所表示的有理数分别是x、y,且|x|=2,|y|=3,则A、B两点间的距离是( )
| A、5 | B、1 |
| C、5或1 | D、以上都不对 |
下列实数中,无理数是( )
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
圆锥的高是4cm,母线长5cm,则其侧面展开图的面积为( )
| A、30πcm2 |
| B、24πcm2 |
| C、15πcm2 |
| D、18πcm2 |
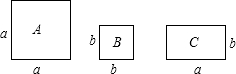 如图所示,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼成一个长为(a+2b)、宽为(2a+b)的大长方形,则需要C类卡片
如图所示,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼成一个长为(a+2b)、宽为(2a+b)的大长方形,则需要C类卡片 在矩形ABCD中,AB=4cm,BC=8cm,E、F分别是AD、BC上两点,并且AC垂直平分EF,垂足为O.
在矩形ABCD中,AB=4cm,BC=8cm,E、F分别是AD、BC上两点,并且AC垂直平分EF,垂足为O. 如图,已知AD、BC相交于点O,AB=CD,AD=CB.试问∠A等于∠C吗?为什么?
如图,已知AD、BC相交于点O,AB=CD,AD=CB.试问∠A等于∠C吗?为什么?