Question

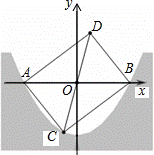
如图，在平面直角坐标系xoy中，已知点A（2，1）、B（﹣1，1）、C（﹣1，﹣3）、D（2，﹣3），把一根长为2015个单位长度没有弹性的细线（线的粗细忽略不计）的一端固定在D处，并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标为　

Answer 1

（2，﹣2）　．    解：∵A（2，1）、B（﹣1，1）、C（﹣1，﹣3）、D（2，﹣3），

∴AB=2﹣（﹣1）=3，BC=1﹣（﹣3）=4，CD=2﹣（﹣1）=3，DA=1﹣（﹣3）=4，

∴绕四边形ABCD一周的细线长度为3+4+3+4=14，

2015÷14=143…13，

∴细线另一端在绕四边形第143圈的第13个单位长度的位置，

即从点D向左沿D→C→B→A→D第13个单位所在的点的坐标即为所求，也就是点（2，﹣2）．

故答案为：（2，﹣2）．