题目内容
某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,求点C关于原点O的对称点D;
(3)写出四边形ACBD的面积.
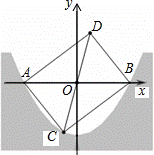
解:(1)根据题意得:OA=OB= AB=4,
AB=4,
∴B点坐标(4,0)
∴0=16a﹣4,
解得:a=
∴此二次函数的解析式为:y= x2﹣4.
x2﹣4.
(2)∵点C(一1,m)是抛物线上一点
∴m= ﹣4=﹣
﹣4=﹣ ,
,
又∵点D与点C关于原点中心对称
∴D点坐标(﹣1,﹣ ).
).
(3)S四边形ACBD=4× ×4×
×4× =30.
=30.

练习册系列答案
相关题目
 交于点A(1,0)和点B,与抛物线的对称轴x=﹣2交于点C(﹣2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.
交于点A(1,0)和点B,与抛物线的对称轴x=﹣2交于点C(﹣2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.
 •
•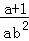 ,并选择你喜欢的整数a,b代入求值.
,并选择你喜欢的整数a,b代入求值.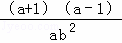 …①
…①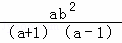 …②
…②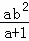 …③
…③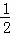 …④
…④
 +
+ 的值为( )
的值为( ) B.
B.  C. ﹣
C. ﹣

 B.
B.  C.
C.  D.
D. 

 二次方程
二次方程 ,必有实数解.”是假命题.则在下列选项中,可以作为反例的是( )
,必有实数解.”是假命题.则在下列选项中,可以作为反例的是( )