题目内容
 已知扇形的半径R=30cm,面积S=300πcm2.
已知扇形的半径R=30cm,面积S=300πcm2.(1)求扇形的弧长;
(2)若将此扇形卷成一个圆锥(无底,忽略接头部分),则这个圆锥的高是多少?
考点:圆锥的计算,弧长的计算,扇形面积的计算
专题:
分析:(1)直接利用扇形的面积公式计算扇形的弧长即可;
(2)利用圆锥的侧面展开图的弧长等于圆锥的底面周长可得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
(2)利用圆锥的侧面展开图的弧长等于圆锥的底面周长可得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
解答:解:(1)∵扇形的半径R=30cm,面积S=300πcm2.
∴扇形的弧长l=
=
=20πcm;
(2)设圆锥的底面半径为r,根据题意,得2πr=20π
∴r=10cm.
∴圆锥的高为
=20
cm,
∴圆锥的高为20
cm.
∴扇形的弧长l=
| 2S |
| R |
| 600π |
| 30 |
(2)设圆锥的底面半径为r,根据题意,得2πr=20π
∴r=10cm.
∴圆锥的高为
| 302-102 |
| 2 |
∴圆锥的高为20
| 2 |
点评:考查圆锥的计算;用到的知识点为:圆锥的弧长=
;圆锥的侧面展开图的弧长等于圆锥的底面周长.
| nπr |
| 180 |

练习册系列答案
相关题目
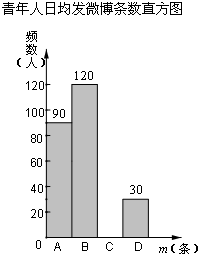 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
 如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?
如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?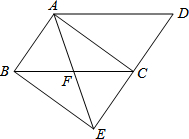 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
 七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理. 如图,△ABC是等边三角形,将△ABP绕点A按逆时针方向旋转后,能与△ACP′重合.如果AP=3,则PP′=
如图,△ABC是等边三角形,将△ABP绕点A按逆时针方向旋转后,能与△ACP′重合.如果AP=3,则PP′=