题目内容
3.已知$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0,求$\frac{xy+yz+zx}{{x}^{2}+{y}^{2}+{z}^{2}}$的值.分析 根据比例的性质,可用x表示y,用x表示z,根据分式的性质,可得答案.
解答 解:由$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0,得
y=$\frac{3x}{2}$,z=2x.
$\frac{xy+yz+zx}{{x}^{2}+{y}^{2}+{z}^{2}}$=$\frac{x•\frac{3x}{2}+\frac{3x}{2}•2x+2x•x}{{x}^{2}+(\frac{3x}{2})^{2}+(2x)^{2}}$=$\frac{\frac{13{x}^{2}}{2}}{\frac{29{x}^{2}}{4}}$=$\frac{26}{29}$.
点评 本题考查了比例的性质,利用比例的性质得出y=$\frac{3x}{2}$,z=2x是解题关键,又利用了分式的性质.

练习册系列答案
相关题目
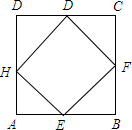 如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.
如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.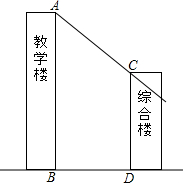 如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)
如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)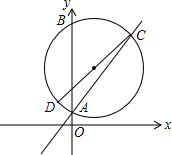 如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.
如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.