题目内容
4.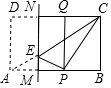 如图,在矩形ABCD中,AB=4,BC=3,点E为对角线AC上一动点(不与点A、C重合),过点E作直线MN∥BC,分别交AB、CD于点M、N,将矩形ADNM沿MN折叠,使得点A、D的对应点P、Q分别落在AB、CD所在的直线上,若△ACP为等腰三角形,则BM的长为$\frac{39}{16}$或$\frac{3}{2}$.
如图,在矩形ABCD中,AB=4,BC=3,点E为对角线AC上一动点(不与点A、C重合),过点E作直线MN∥BC,分别交AB、CD于点M、N,将矩形ADNM沿MN折叠,使得点A、D的对应点P、Q分别落在AB、CD所在的直线上,若△ACP为等腰三角形,则BM的长为$\frac{39}{16}$或$\frac{3}{2}$.
分析 分两种情形①当PA=PC时,设PA=PC=x,在Rt△PBC中,构建PC2=BP2+BC2,可得x2=32+(4-x)2,求出x即可解决问题.②当AP=AC时,AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,可得AP=5,PM=AM=$\frac{5}{2}$,由此即可求出BM.
解答 解: ①当PA=PC时,设PA=PC=x,
①当PA=PC时,设PA=PC=x,
在Rt△PBC中,∵PC2=BP2+BC2,
∴x2=32+(4-x)2,
∴x=$\frac{25}{8}$,
∴PM=AM=$\frac{1}{2}$PA=$\frac{25}{16}$,
∴BM=AB-AM=4-$\frac{25}{16}$=$\frac{39}{16}$
②当AP=AC时,
∵AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AP=5,
∴PM=AM=$\frac{5}{2}$,
∴BM=AB=AM=4-$\frac{5}{2}$=$\frac{3}{2}$,
故答案为$\frac{39}{16}$或$\frac{3}{2}$.
点评 本题考查翻折变换、矩形的性质、等腰三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | m6÷m2=m3 | B. | 3m3-2m2=m | C. | (3m2)3=27m6 | D. | $\frac{1}{2}$m•2m2=m2 |
12.使二次根式$\sqrt{x-7}$有意义的x的取值范围是( )
| A. | 1<x<7 | B. | 0<x≤7 | C. | x≤7 | D. | x≥7 |
8. 如图是一个正方体的表面展开图,则原正方体中与“凉”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“凉”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“凉”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“凉”字所在的面相对的面上标的字是( )| A. | 凉 | B. | 都 | C. | 六 | D. | 好 |
 如图,在△ABC中,AB=AC,D为BC的中点,且∠BAD=25°,则∠C的度数是65°.
如图,在△ABC中,AB=AC,D为BC的中点,且∠BAD=25°,则∠C的度数是65°. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB. 如图,已知CD是⊙O的直径,AB是⊙O的弦且AB=16cm,AB⊥CD,垂足为M,OM:MC=3:2,则CD的长为20cm.
如图,已知CD是⊙O的直径,AB是⊙O的弦且AB=16cm,AB⊥CD,垂足为M,OM:MC=3:2,则CD的长为20cm.