题目内容
9.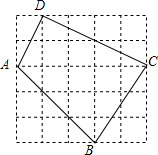 如图,每个小方格的边长都为1.
如图,每个小方格的边长都为1.(1)求证:∠ADC=90°;
(2)求图中格点四边形ABCD的周长和面积.
分析 (1)由勾股定理求出AD2、CD2的长,得出AD2+CD2=AC2,根据勾股定理的逆定理即可证明∠ADC=90°;
(2)由勾股定理求出AB、BC的长,由(1)得出AD、CD的长,将四边相加即可得出四边形ABCD的周长;根据四边形ABCD的面积=大正方形的面积-4个直角三角形的面积,列式计算即可.
解答 (1)证明:由勾股定理得:AD2=12+22=5,CD2=42+22=20,
∴AD2+CD2=5+20=25,
∴AD2+CD2=AC2,
∴∠ADC=90°;
(2)解:由勾股定理得:AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵AD2=5,CD2=20,
∴AD=$\sqrt{5}$,CD=2$\sqrt{5}$,
∴四边形ABCD的周长=3$\sqrt{2}$+$\sqrt{13}$+2$\sqrt{5}$+$\sqrt{5}$=3$\sqrt{2}$+$\sqrt{13}$+3$\sqrt{5}$;
四边形ABCD的面积=5×5-$\frac{1}{2}$×3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×1=12.5.
点评 本题考查了勾股定理、勾股定理的逆定理、三角形和四边形面积的计算;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
18.7x+1是不小于-3的负数,表示为( )
| A. | -3≤7x+1≤0 | B. | -3<7x+1<0 | C. | -3≤7x+1<0 | D. | -3<7x+1≤0 |
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发去乙地.如图,线段OA表示货车离开甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离开甲地的距离y(千米)与时间x(小时)之间的函数关系.
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发去乙地.如图,线段OA表示货车离开甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离开甲地的距离y(千米)与时间x(小时)之间的函数关系.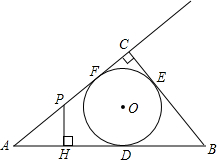 如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.