题目内容
7.定义:到三角形两边距离相等的点叫做三角形的准内心.已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点P△ABC的准内心(不包括顶点),且点P在△ABC的边上,则CP的长为$\frac{24}{7}$或$\frac{8}{3}$或$\frac{5}{3}$.分析 分三种情形①点P在AB边上,②点P在AC边上,③点P在BC边上,分别讨论计算即可.
解答 解:
如图3中,
当点P在AB边上时,∵AC=6,BC=8,∠ACB=90°,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵点P是△ABC的准内心,
∴∠PCB=∠PCA=45°,
∴PC=$\frac{24}{7}$;
如图4中,当点P在AC边上时,作PE⊥AB于E,设PE=x,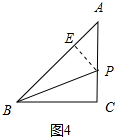
∵点P是△ABC的准内心,
∴∠PBA=∠PBC,
∵PE⊥AB,PC⊥BC,
∴PE=PC=x,BE=BC=8,
∴AE=2,
∴22+x2=(6-x)2,
解得:x=$\frac{8}{3}$;
如图5中,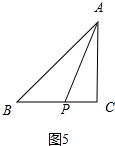
当点P在BC边上时,同理可得PC=$\frac{5}{3}$;
故答案为:$\frac{24}{7}$或$\frac{8}{3}$或$\frac{5}{3}$.
点评 本题考查角平分线的性质、勾股定理、三角形的准内心的定义等知识,解题的关键是理解题意,学会分类讨论,属于中考常考题型.

练习册系列答案
相关题目
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 线段 | B. | 等边三角形 | C. | 五角星 | D. | 等腰梯形 |
19.已知$\sqrt{x+2}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≠-2 | C. | x>-2 | D. | x≥2 |
16.方程2x2-5x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 两根异号 |
12.2a=3,2b=6,2c=12,则a,b,c大小关系为( )
| A. | 2b<a+c | B. | 2b=a+c | C. | 2b>a+c | D. | a+b=c |
 如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由.
如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由. △ABC中,AB=18cm,BC=6cm,BD平分∠ABC交AC于D,DE⊥AB于E,S△ABC=36cm2,则DE=3cm.
△ABC中,AB=18cm,BC=6cm,BD平分∠ABC交AC于D,DE⊥AB于E,S△ABC=36cm2,则DE=3cm. 如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是6.
如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是6.