题目内容
19. 如图,在?ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.
如图,在?ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.(1)求证:△ADE≌△FCE;
(2)连结AC、DF,判断四边形ACFD是什么四边形?说明理由.
分析 (1)由平行四边形的性质和中点的性质,易得∠DAE=∠F,∠D=∠ECF,AE=CE,继而证得:△ADE≌△FCE.
(2)由第(1)问中△ADE≌△FCE,易得AD=CF,又由AD∥CF,即可证得四边形ACFD是平行四边形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠F,∠D=∠ECF,
又∵E是DC的中点,
∴DE=CE,
在△ADE和△FCE中,
$\left\{\begin{array}{l}{∠DAE=∠F}\\{AE=CE}\\{∠D=∠ECF}\end{array}\right.$,
∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,
∴AD=CF,
又∵AD∥CF,
∴四边形ACFD是平行四边形.
点评 此题考查了平行四边形的判定与性质以及全等三角形的判定与性质.注意有一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.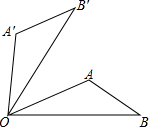 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )
 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )| A. | 60° | B. | 45° | C. | 35° | D. | 25° |
4. 有理数a、b在数轴上的对应的位置如图所示:则( )
有理数a、b在数轴上的对应的位置如图所示:则( )
 有理数a、b在数轴上的对应的位置如图所示:则( )
有理数a、b在数轴上的对应的位置如图所示:则( )| A. | a-b>0 | B. | a+b>0 | C. | a•b>0 | D. | $\frac{b}{a}>0$ |
8.下列说法中正确的是( )
| A. | -0.064的立方根是0.4 | B. | -9的平方根是±3 | ||
| C. | 0.001的立方根是0.000001 | D. | 16的立方根是$\root{3}{16}$ |
 +
+ =___________
=___________ 是一元二次方程,则
是一元二次方程,则 的值为( )
的值为( ) B. 2 C. -2 D. 以上都不对
B. 2 C. -2 D. 以上都不对 如图,AC∥CD,点E在BC上,若∠D=∠DEC=74°,求∠B的度数.
如图,AC∥CD,点E在BC上,若∠D=∠DEC=74°,求∠B的度数. 有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了7个单位长度到达点C处,蚂蚁乙从图中点B的位里沿数轴向左爬了5个单位长度到达点D处.
有两只小蚂蚁在如图所示的数轴上爬行,蚂蚁甲从图中点A的位置沿数轴向右爬了7个单位长度到达点C处,蚂蚁乙从图中点B的位里沿数轴向左爬了5个单位长度到达点D处.