题目内容
15．若方程组$\left\{\begin{array}{l}{4x+3m=2}\\{8x-3y=m}\end{array}\right.$的解满足x＞2y，求m的取值范围．分析 根据加减消元法，可得方程组的解，根据解不等式，可得答案．
解答 解：$\left\{\begin{array}{l}{4x+3m=2①}\\{8x-3y=m②}\end{array}\right.$
由①得
x=$\frac{2-3m}{4}$ ③，
把③代入②，得
y=$\frac{4-7m}{3}$，
由x＞2y，得
$\frac{2-3m}{4}$＞$\frac{8-14m}{3}$，
解得m＞$\frac{26}{45}$．
点评 本题考查了二元一次方程组的解，利用方程组的解得出不等式是解题关键．
练习册系列答案
相关题目
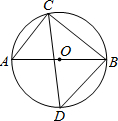如图，AB是⊙O的直径，CD平分∠ACB交⊙O于点D，BD=5cm，求∠ABD的度数及AB的长．
如图，在△ABC中，M是AB的中点，过M的直线交BC于E，过A作AP∥BC交ME于P，过M作FM⊥PE，交AC于F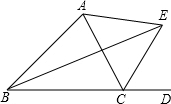
已知△ABC中，∠ACD是外角，BE平分∠ABC，CE平分∠ACD，∠BEC=42°．