题目内容
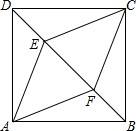 如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF.
如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF.(1)四边形AECF是什么四边形?请证明.
(2)若EF=4,DE=BF=2,求四边形AEBF的周长.
考点:正方形的性质,菱形的判定与性质
专题:
分析:(1)由对角线互相垂直平分的四边形是菱形,AO=CO,EO=FO,AC⊥EF即可证得.
(2)根据正方形性质得出AC⊥BD,AC=BD,OA=OB=OC=OD,根据已知得出AC=BD=8,OA=OD=4,OE=2,然后根据勾股定理即可求得AE的值,进而求得四边形AEBF的周长.
(2)根据正方形性质得出AC⊥BD,AC=BD,OA=OB=OC=OD,根据已知得出AC=BD=8,OA=OD=4,OE=2,然后根据勾股定理即可求得AE的值,进而求得四边形AEBF的周长.
解答: (1)答:四边形AECF为菱形.
(1)答:四边形AECF为菱形.
证明:连接AC,
∵四边形ABCD是正方形,
∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴DE=BF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴四边形AECF为菱形.
(2)解:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OB=OC=OD,
∵EF=4,DE=BF=2,
∴AC=BD=8,OA=OD=4,
∴OE=2,
在RT△AOE中,AE=
=
=2
,
∴四边形AEBF的周长=4×2
=8
.
 (1)答:四边形AECF为菱形.
(1)答:四边形AECF为菱形.证明:连接AC,
∵四边形ABCD是正方形,
∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴DE=BF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴四边形AECF为菱形.
(2)解:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OB=OC=OD,
∵EF=4,DE=BF=2,
∴AC=BD=8,OA=OD=4,
∴OE=2,
在RT△AOE中,AE=
| OA2+OE2 |
| 42+22 |
| 5 |
∴四边形AEBF的周长=4×2
| 5 |
| 5 |
点评:本题考查了正方形对角线互相垂直平分的性质,考查了菱形的判定以及勾股定理的应用,本题中证明AC与EF互相垂直平分是解题的关键.

练习册系列答案
相关题目
若3x2n-7-1=5是关于x的一元一次方程,则n的值( )
| A、2 | B、3 | C、4 | D、5 |
 如图,点A、B、C三点均在⊙O上,∠B=∠C.以下结论错误的是( )
如图,点A、B、C三点均在⊙O上,∠B=∠C.以下结论错误的是( )| A、AB=AC | ||||
B、
| ||||
C、
| ||||
| D、∠BOC=80° |

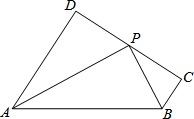 如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?
如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?