题目内容
解方程:
(1)x2-2x-3=0;
(2)3x2+x-1=0.
(1)x2-2x-3=0;
(2)3x2+x-1=0.
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:
分析:(1)利用“十字相乘法”对等式的左边进行因式分解;
(2)利用求根公式x=
来解方程.
(2)利用求根公式x=
-b±
| ||
| 2a |
解答:解:(1)由原方程,得
(x-3)(x+1)=0,
则x-3=0或x+1=0,
解得 x1=3,x2=-1;
(2)∵a=3,b=1,c=-1,
∴x=
=
,
解得x1=
,x2=
.
(x-3)(x+1)=0,
则x-3=0或x+1=0,
解得 x1=3,x2=-1;
(2)∵a=3,b=1,c=-1,
∴x=
-b±
| ||
| 2a |
-1±
| ||
| 6 |
解得x1=
-1+
| ||
| 6 |
-1-
| ||
| 6 |
点评:本题考查了方程的解法:因式分解法和公式法.理解公式x=
中的字母所表示的含义是解方程的关键.
-b±
| ||
| 2a |

练习册系列答案
相关题目
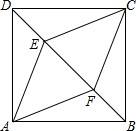 如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF.
如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF. 如图,在△ABC与△AED中,AB=AE,AC=AD,请补充一个已知条件:
如图,在△ABC与△AED中,AB=AE,AC=AD,请补充一个已知条件: