题目内容
8. 如图,点M是直线y=2x+3在第二象限上的动点,过点M作MN垂直x轴于点N,在y轴的正半轴上求点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标(0,0)、(0,1)或(0,$\frac{3}{4}$).
如图,点M是直线y=2x+3在第二象限上的动点,过点M作MN垂直x轴于点N,在y轴的正半轴上求点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标(0,0)、(0,1)或(0,$\frac{3}{4}$).
分析 设点M的坐标为(m,2m+3),由点M在第二象限且在直线y=2x+3上,利用一次函数图象上点的坐标特征即可得出m的取值范围,分∠MNP=90°、∠NMP=90°以及∠MPN=90°三种情况考虑,利用等腰直角三角形的性质找出点M的坐标,将其代入一次函数解析式中求出m值,由此即可得出点P的坐标.
解答 解:设点M的坐标为(m,2m+3),
令y=2x+3>0,解得:x>-$\frac{3}{2}$,
∴-$\frac{3}{2}$<x<0.
当∠MNP=90°时,MN=ON,
∴点M的坐标为(m,-m),
∵点M在直线y=2x+3上,
∴-m=2m+3,
解得:m=-1,
∴点P的坐标为(0,0);
当∠NMP=90°时,MN=PM,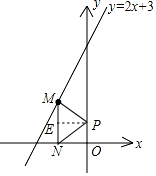
∴点M的坐标为(m,-m),
∵点M在直线y=2x+3上,
∴-m=2m+3,
解得:m=-1,
∴点P的坐标为(0,1);
当∠MPN=90°时,过点P作PE⊥MN于点E,
∵△MNP为等腰直角三角形,
∴MN=2PE,
∴点M的坐标为(m,-2m),
∵点M在直线y=2x+3上,
∴-2m=2m+3,
解得:m=-$\frac{3}{4}$,
∴点P的坐标为(0,$\frac{3}{4}$).
综上可知:符合条件的点P的坐标为(0,0)、(0,1)或(0,$\frac{3}{4}$).
点评 本题考查了一次函数图象上点的坐标特征以及等腰直角三角形的性质,分∠MNP=90°、∠NMP=90°以及∠MPN=90°三种情况考虑是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.一组数据1、2、4、4、3的众数为4,则这组数据的中位数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知-6a9b4和5a4nb4是同类项,则代数式12n-10的值是( )
| A. | 17 | B. | 37 | C. | -17 | D. | 98 |
17.近几年,我国经济高速发展,但退休人员待遇持续偏低,为了促进社会公平,国家决定大幅增加退休人员退休金,深圳企业退休职工李师傅2014年月退休金为3500元,2016年达到4200元,设李师傅的月退休金从2014年到2016年年平均增长率为x,可列方程为( )
| A. | 3500(1+x)=4200 | B. | 3500(1-x)+3500(1-x)2=4200 | ||
| C. | 3500(1-x)=4200 | D. | 3500(1-x)2=4200 |
19.化简-16(x-$\frac{1}{2}$)的结果是( )
| A. | -16x-$\frac{1}{2}$ | B. | -16x+$\frac{1}{2}$ | C. | -16x-8 | D. | -16x+8 |

 已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.
已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.