题目内容
13.四边形ABCD和四边形DEFG都是正方形,点H是BF的中点,连接HA,HG.(1)若三点B、D、F在同一直线上,如图1,探索HA、HG的数量和位置关系,并给予证明;
(2)如图2,若三点B、D、F不在同一直线上,那么(1)中的结论是否仍然成立?请说明理由.

分析 (1)如图1,延长AH,FE交于点M,连接GM,AG,根据正方形的性质得到AB=AD,∠ADB=∠GDF=∠ABD=∠DFE=45°,得到∠ADG=90°,推出△ABH≌△HMF,根据全等角形的性质得到AB=MF,AH=HM,等量代换得到AD=MF,推出△AGD≌△GMF,
由全等三角形的性质得到AG=GM,∠AGD=∠FGM,于是得到∠AGM=90°,推出△AGM是等腰直角三角形,即可得到结论;
(2)如图2,延长AH到M使HM=AH,连接AG,FM,GM,FM交DE于K,通过△ABH≌△HMF,得到AB=MF,AH=HM,∠ABH=∠HFM,证得AD=MF,AB∥FM,推出∠DKM=∠ADG,根据平行线的性质得到∠GFM=∠DKM,等量代换得到∠ADG=∠GFM,证得△AGD≌△GMF,由全等三角形的性质得到AG=GM,∠AGD=∠FGM推出△AGM是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.
解答 解:(1)如图1,延长AH,FE交于点M,连接GM,AG,
∵四边形ABCD和四边形DEFG都是正方形,
∴AB=AD,∠ADB=∠GDF=∠ABD=∠DFE=45°,
∴∠ADG=90°,
在△ABH与△HMF中,$\left\{\begin{array}{l}{∠AHB=∠MHF}\\{BH=FH}\\{∠ABH=∠HFM}\end{array}\right.$,
∴△ABH≌△HMF,
∴AB=MF,AH=HM,
∴AD=MF,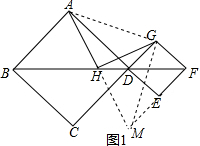
在△AGD与△GMF中,$\left\{\begin{array}{l}{AD=MF}\\{∠ADG=∠GFM=90°}\\{DG=DE}\end{array}\right.$,
∴△AGD≌△GMF,
∴AG=GM,∠AGD=∠FGM,
∵∠FGM+∠DGM=90°,
∴∠AGD+∠DGM=90°,
∴∠AGM=90°,
∴△AGM是等腰直角三角形,
∴AH=HG,GH⊥AM;
(2)(1)中的结论仍然成立,
理由:如图2,延长AH到M使HM=AH,连接AG,FM,GM,FM交DE于K,
在△ABH与△HMF中,$\left\{\begin{array}{l}{AH=HM}\\{∠AHB=∠FHM}\\{BH=FH}\end{array}\right.$,
∴△ABH≌△HMF,
∴AB=MF,AH=HM,∠ABH=∠HFM,
∴AD=MF,AB∥FM,
∴FM∥CD,
∴∠MKD+∠CDE=180°,
∵∠ADG+∠CDE=180°,
∴∠DKM=∠ADG,
∵GF∥DE,
∴∠GFM=∠DKM,
∴∠ADG=∠GFM,
在△AGD与△GMF中,$\left\{\begin{array}{l}{AD=MF}\\{∠ADG=∠GFM}\\{DG=DE}\end{array}\right.$,
∴△AGD≌△GMF,
∴AG=GM,∠AGD=∠FGM,
∵∠FGM+∠DGM=90°,
∴∠AGD+∠DGM=90°,
∴∠AGM=90°,
∴△AGM是等腰直角三角形,
∴AH=HG,GH⊥AM.
点评 本题考查了全等三角形的判定和性质,正方形的性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.

| A. | 第一次向右拐50°第二次向左拐130° | |
| B. | 第一次向左拐30°第二次向右拐30° | |
| C. | 第一次向右拐50°第二次向右拐130° | |
| D. | 第一次向左拐50°第二次向左拐130° |
 如图,请按照要求回答问题.
如图,请按照要求回答问题.
 如图,AB=AC,BD⊥AC,垂足为D,CE⊥AB.垂足为E,BD和CE相交于点F,那么∠BAF与∠CAF相等吗?说明理由.
如图,AB=AC,BD⊥AC,垂足为D,CE⊥AB.垂足为E,BD和CE相交于点F,那么∠BAF与∠CAF相等吗?说明理由.
 如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD,BE交于O点.求证:BO=CO.
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD,BE交于O点.求证:BO=CO.