题目内容
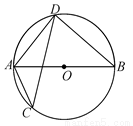
18. 如图,己知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
如图,己知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
分析 由∠1=∠2可得∠BAC=∠DAE,只需运用“AAS”即可证到△ABC和△ADE全等.
解答 解:△ABC和△ADE全等.
理由如下:
∵∠1=∠2,
∴∠BAC=∠DAE.
在△ABC和△ADE中,
$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{∠C=∠E}\\{AB=AD}\end{array}\right.$,
∴△ABC≌△ADE(AAS).
点评 本题主要考查的是两个三角形全等的判定,需要注意的是∠1与∠2不是△ABC和△ADE中的对应角,不能由∠1=∠2直接证到△ABC≌△ADE,而应由∠1=∠2证到△ABC和△ADE中的对应角∠BAC与∠DAE相等才行.

练习册系列答案
相关题目
8.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=k-2}\\{3x+2y=-4}\end{array}\right.$的解满足x+y>1,则实数k的取值范围是( )
| A. | k<0 | B. | k<-1 | C. | k<-2 | D. | k<-3 |
6.若关于x、y的方程组$\left\{\begin{array}{l}{x+3y=3}\\{3x+y=m+1}\end{array}\right.$的解有x+y>0,则m的取值范围是( )
| A. | m>4 | B. | m<4 | C. | m>-4 | D. | m<-4 |
13.如图,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
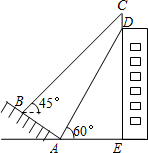 如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图所示,直线AB与EF交于点O,已知∠AOD=∠COE=90°,写出图中与∠COD互余的角,这些角之间有什么关系?根据是什么?
如图所示,直线AB与EF交于点O,已知∠AOD=∠COE=90°,写出图中与∠COD互余的角,这些角之间有什么关系?根据是什么?