题目内容
16.若△ABC∽△A′B′C′,且△ABC的三边长分别为$\sqrt{3}$、2、$\sqrt{5}$,△A′B′C′的两边长分别为$\sqrt{6}$、$\sqrt{10}$,则其第三边的长为2$\sqrt{2}$.分析 设△A′B′C′第三边的长为x,根据相似三角形的性质得出比例式,即可求出x.
解答 解:设△A′B′C′第三边的长为x,
∵△ABC∽△A′B′C′,△ABC的三边长分别为$\sqrt{3}$、2、$\sqrt{5}$,△A′B′C′的两边长分别为$\sqrt{6}$、$\sqrt{10}$,
∴$\frac{\sqrt{3}}{\sqrt{6}}$=$\frac{\sqrt{5}}{\sqrt{10}}$=$\frac{2}{x}$,
解得:x=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了相似三角形的性质的应用,能得出比例式是解此题的关键,注意:相似三角形的对应边的比相等.

练习册系列答案
相关题目
6.一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:

请观察表中数据规律填表:

请观察表中数据规律填表:
| 餐桌张数 | 1 | 2 | 3 | 4 | …n |
| 可坐人数 | 6 | 8 | 10 | 12 | 2n+4 |
 元旦晚会上,小刚用一张半径为25cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的圆心角应为144度.
元旦晚会上,小刚用一张半径为25cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的圆心角应为144度.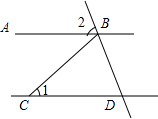 如图所示,AB∥CD,BC=CD,∠1=40°,则∠2的度数为70°.
如图所示,AB∥CD,BC=CD,∠1=40°,则∠2的度数为70°. 如图,已知⊙O1与⊙O2交于点A、B,CD是两圆的外公切线,切点为C、D,直线BC与AD、BD与AC分别交于点E、F,求证:$\frac{EA}{AF}$=$\frac{FB}{BE}$.
如图,已知⊙O1与⊙O2交于点A、B,CD是两圆的外公切线,切点为C、D,直线BC与AD、BD与AC分别交于点E、F,求证:$\frac{EA}{AF}$=$\frac{FB}{BE}$.