题目内容
5. 如图,直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$只有一个公共点A(1,-2).
如图,直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$只有一个公共点A(1,-2).(1)求k与a的值;
(2)若直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$有两个公共点,请直接写出b的取值范围.
分析 (1)把点A坐标分别代入直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$求出k和a的值即可;
(2)根据根的判别式即可得出结果.
解答 解:(1)∵直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$只有一个公共点A(1,-2).
∴$\left\{\begin{array}{l}{-2=a-4}\\{-2=\frac{k}{1}}\end{array}\right.$,解得:a=2,k=-2;
(2)若直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$有两个公共点,
则方程组$\left\{\begin{array}{l}{y=2x-2}\\{y=-\frac{2}{x}}\end{array}\right.$有两个不同的解,
∴2x+b=-$\frac{2}{x}$有两个不相等的解,
整理得:2x2+bx+2=0,
∴△=b2-16>0,
解得:b<-4,或b>4.
点评 本题考查了反比例函数与一次函数的交点问题,平移的性质,一元二次方程根的判别式;知道反比例函数的图象与直线y=kx+4(k≠0)有两个公共点时,△>0是解决问题(2)的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
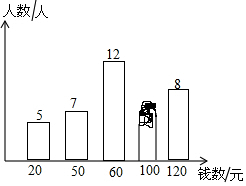 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.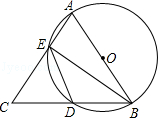 如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE.
如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).