题目内容
已知，AD是△ABC的高，E是BC的中点，EF⊥BC交AC于F，若BD=
，DC=3，AC=5，则线段AF的长为 ．
| 5 |
| 3 |
考点：相似三角形的判定与性质,勾股定理
专题：
分析：根据题意，作如下图形，由勾股定理可求得AD的长，再由EF∥AD，根据平行线分线段成比例定理，即可求出线段AF的长度．
解答：解：如图所示，∵AD是△ABC的高，
∴AD⊥BC，DC=3，AC=5，
∴AD=
=
=4，
又∵E是BC的中点，BD=
，
∴EC=
，
又∵EF⊥BC，
∴EF∥AD，
∴
=
，即：
=
解得：CF=
，
所以AF=CA-CF=5-
=
．
故答案为：
．
解：如图所示，∵AD是△ABC的高，∴AD⊥BC，DC=3，AC=5，
∴AD=
| AC2-DC2 |
| 52-32 |
又∵E是BC的中点，BD=
| 5 |
| 3 |
∴EC=
| 7 |
| 3 |
又∵EF⊥BC，
∴EF∥AD，
∴
| CE |
| CD |
| CF |
| CA |
| ||
| 3 |
| CF |
| 5 |
解得：CF=
| 35 |
| 9 |
所以AF=CA-CF=5-
| 35 |
| 9 |
| 10 |
| 9 |
故答案为：
| 10 |
| 9 |
点评：本题考查了勾股定理以及平行线分线段成比例定理的综合应用，属于基础题目．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
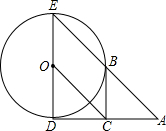如图，已知⊙O的半径为1，DE是⊙O的直径，过D点作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，若四边形BCOE是平行四边形，
一次函数y=kx+b的图象如图所示，则k
如图，已知点A为反比例函数y=
将一张长方形的白纸如图形式折叠，使D到Dˊ，E到Eˊ处，并且BDˊ与BEˊ在同一条直线上，那么AB与BC的位置的关系是