题目内容
 将一张长方形的白纸如图形式折叠,使D到Dˊ,E到Eˊ处,并且BDˊ与BEˊ在同一条直线上,那么AB与BC的位置的关系是
将一张长方形的白纸如图形式折叠,使D到Dˊ,E到Eˊ处,并且BDˊ与BEˊ在同一条直线上,那么AB与BC的位置的关系是考点:角的计算,垂线,翻折变换(折叠问题)
专题:
分析:根据折叠可得出∠ABD=ABD′,∠EBC=∠E′BC,再由∠ABD+ABD′+∠EBC+∠E′BC=180°,从得出ABD′+∠EBC=90°,可得出AB⊥BC.
解答:解:由折叠可得,∠ABD=ABD′,∠EBC=∠E′BC,
∵∠ABD+ABD′+∠EBC+∠E′BC=180°,
∴ABD′+∠EBC=90°,
∴AB⊥BC.
∴AB与BC的位置的关系是垂直,
故答案为AB⊥BC.
∵∠ABD+ABD′+∠EBC+∠E′BC=180°,
∴ABD′+∠EBC=90°,
∴AB⊥BC.
∴AB与BC的位置的关系是垂直,
故答案为AB⊥BC.
点评:本题考查了角的计算、垂线以及翻折变换,是基础知识,要熟练掌握.

练习册系列答案
相关题目
已知a=234,b=243,c=324,d=432,e=423,则a,b,c,d,e的大小关系是( )
| A、a=b=d=e<c |
| B、a=b=d=e>c |
| C、e<d<c<b<a |
| D、e<c<d<b<a |
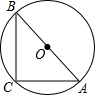 如图,AB是⊙O的直径,∠B=45°,AB=2,则∠C=
如图,AB是⊙O的直径,∠B=45°,AB=2,则∠C=