题目内容
20. 如图所示,有一圆弧形拱桥,其跨度AB=10m,拱高为1m,
如图所示,有一圆弧形拱桥,其跨度AB=10m,拱高为1m,(1)请你确定圆弧所在圆的圆心;
(2)求拱桥所在圆的直径长.
分析 (1)根据弦的垂直平分线都经过圆心来作.作AB的垂直平分线MN,交弧于C,连接BC,作BC的垂直平分线EF,MN与EF相交于O,点O就是所求的圆心.
(2)连接OC,设这个门拱的半径为r,则OD=r-1,根据垂径定理得到AD=BD=$\frac{1}{2}$AB,在Rt△OAD中,由勾股定理得OA2=AD2+OD2,然后即可得到关于r的方程,解方程即可求出2r.
解答 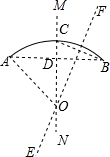 解:(1)根据弦的垂直平分线都经过圆心,作AB的垂直平分线MN,交弧于C,连接BC,作BC的垂直平分线EF,MN与EF相交于O,点O就是所求的圆心.如图,
解:(1)根据弦的垂直平分线都经过圆心,作AB的垂直平分线MN,交弧于C,连接BC,作BC的垂直平分线EF,MN与EF相交于O,点O就是所求的圆心.如图,
(2)连接OC,
设这个拱桥的半径为r,则OD=r-1,
∴AD=BD=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5m
在Rt△OAD中,AD=5m,OD=r-1
由勾股定理得:OA2=AD2+OD2
即r2=52+(r-1)2
∴2r=26m.
这个拱桥所在圆的直径长为26m.
点评 本题考查了垂径定理的应用,勾股定理的应用,解答此题关键是连接OC,构造出直角三角形利用勾股定理解答.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
10.若(x-4)(x+n)=x2+mx-32,则m、n的值分别是( )
| A. | 4,8 | B. | 4,-8 | C. | -4,8 | D. | -4,-8 |
11.下列四个数是负分数的是( )
| A. | -(-0.6$\stackrel{•}{6}$) | B. | π | C. | -$\frac{3}{5}$ | D. | 0.341 |
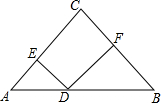 如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8.
如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8.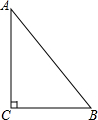 有一块直角三角形的绿地,量得BC、AC两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且要求扩充的绿地部分是以AC为直角边的直角三角形ACD,求扩充后绿地所构成等腰三角形ABD的周长.
有一块直角三角形的绿地,量得BC、AC两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且要求扩充的绿地部分是以AC为直角边的直角三角形ACD,求扩充后绿地所构成等腰三角形ABD的周长.