题目内容
9.(1)如图1,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;(2)如图2,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
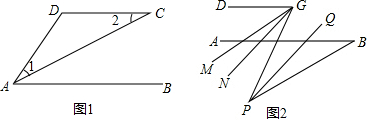
分析 (1)先根据角平分线的性质得出∠1=∠BAC.再由∠1=∠2可知∠BAC=∠2,故可得出结论;
(2)先根据三角形的外角性质,∠1=∠BPG+∠B,再由PQ平分∠BPG,GM平分∠DGP可得出∠GPQ=$\frac{1}{2}$∠BPG,∠MGP=$\frac{1}{2}$∠DGP.根据平行线的性质得出∠1=∠DGP,∠NGP=∠GPQ=$\frac{1}{2}$∠BPG,再利用等量代换即可得出结论.
解答 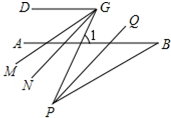 解:(1)AB∥CD.理由如下:
解:(1)AB∥CD.理由如下:
∵AC平分∠DAB,
∴∠1=∠BAC.
∵∠1=∠2,
∴∠BAC=∠2,
∴AB∥CD;
(2)如图,根据三角形的外角性质,∠1=∠BPG+∠B,
∵PQ平分∠BPG,GM平分∠DGP,
∴∠GPQ=$\frac{1}{2}$∠BPG,∠MGP=$\frac{1}{2}$∠DGP.
∵AB∥CD,
∴∠1=∠DGP,
∴∠MGP=$\frac{1}{2}$(∠BPG+∠B).
∵PQ∥GN,
∴∠NGP=∠GPQ=$\frac{1}{2}$∠BPG,
∴∠MGN=∠MGP-∠NGP=$\frac{1}{2}$(∠BPG+∠B)-$\frac{1}{2}$∠BPG=$\frac{1}{2}$∠B=$\frac{1}{2}$×30°=15°,
∴②∠MGN的度数为15°不变.
点评 本题考查的是平行线的判定与性质,熟知内错角相等,两直线平行是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如果把分式中的x和y都扩大2倍,即分式$\frac{xy}{x+y}$的值( )
| A. | 扩大4倍 | B. | 扩大2倍 | C. | 不变 | D. | 缩小2倍 |
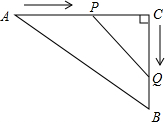 如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?
如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似? 如图,已知△ABC.
如图,已知△ABC.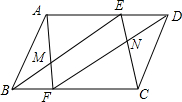 如图,在?ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.
如图,在?ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.