题目内容
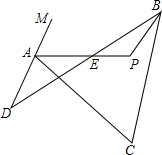 如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=________.
如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=________.
136°
分析:先根据三角形内角和定理得出∠P=180°-∠PBE-∠PEB,再由角平分线的性质可知∠PBE= (180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG=
(180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG= (180°-∠DAG)再把三式联立即可得出结论.
(180°-∠DAG)再把三式联立即可得出结论.
解答: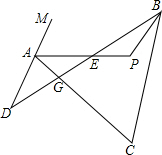 解:∵∠P=180°-∠PBE-∠PEB,
解:∵∠P=180°-∠PBE-∠PEB,
∠PBE= (180°-∠C-∠CGB)①,
(180°-∠C-∠CGB)①,
∠PEB=180°-∠D-∠DAE②,
∠EAG= (180°-∠DAG)③
(180°-∠DAG)③
∴∠P=180°-∠PBE-∠PEB
=180°- (180°-∠C-∠CGB)-∠PEB
(180°-∠C-∠CGB)-∠PEB
=90°+ ∠C+
∠C+ ∠CGB-(180°-∠D-∠DAE)
∠CGB-(180°-∠D-∠DAE)
= ∠C+
∠C+ ∠CGB-90°+∠D+(∠DAG+
∠CGB-90°+∠D+(∠DAG+ ∠CAM)
∠CAM)
= ∠C+
∠C+ ∠CGB-90°+∠D+(180°-∠D-∠DGA)+
∠CGB-90°+∠D+(180°-∠D-∠DGA)+ (∠D+∠DGA)
(∠D+∠DGA)
=90°+ ∠C+
∠C+ ∠D
∠D
=90°+ ×62°+
×62°+ ×30°
×30°
=136°.
故答案为:136°.
点评:本题考查的是三角形外角的性质,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件.
分析:先根据三角形内角和定理得出∠P=180°-∠PBE-∠PEB,再由角平分线的性质可知∠PBE=
 (180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG=
(180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG= (180°-∠DAG)再把三式联立即可得出结论.
(180°-∠DAG)再把三式联立即可得出结论.解答:
 解:∵∠P=180°-∠PBE-∠PEB,
解:∵∠P=180°-∠PBE-∠PEB,∠PBE=
 (180°-∠C-∠CGB)①,
(180°-∠C-∠CGB)①,∠PEB=180°-∠D-∠DAE②,
∠EAG=
 (180°-∠DAG)③
(180°-∠DAG)③∴∠P=180°-∠PBE-∠PEB
=180°-
 (180°-∠C-∠CGB)-∠PEB
(180°-∠C-∠CGB)-∠PEB=90°+
 ∠C+
∠C+ ∠CGB-(180°-∠D-∠DAE)
∠CGB-(180°-∠D-∠DAE)=
 ∠C+
∠C+ ∠CGB-90°+∠D+(∠DAG+
∠CGB-90°+∠D+(∠DAG+ ∠CAM)
∠CAM)=
 ∠C+
∠C+ ∠CGB-90°+∠D+(180°-∠D-∠DGA)+
∠CGB-90°+∠D+(180°-∠D-∠DGA)+ (∠D+∠DGA)
(∠D+∠DGA)=90°+
 ∠C+
∠C+ ∠D
∠D=90°+
 ×62°+
×62°+ ×30°
×30°=136°.
故答案为:136°.
点评:本题考查的是三角形外角的性质,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件.

练习册系列答案
相关题目
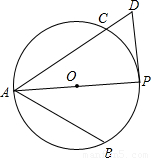
 如图,已知AP平分∠BAC,过P点的切线交AC的延长线于D,如果AB=3cm,AD=6cm,那么AP=
如图,已知AP平分∠BAC,过P点的切线交AC的延长线于D,如果AB=3cm,AD=6cm,那么AP= 如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=
如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P= 如图,已知AP平分∠BAC,过P点的切线交AC的延长线于D,如果AB=3cm,AD=6cm,那么AP=________.
如图,已知AP平分∠BAC,过P点的切线交AC的延长线于D,如果AB=3cm,AD=6cm,那么AP=________.