题目内容
5.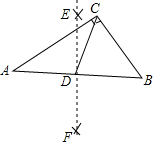 如图,在△ABC中,∠ACB=90°,按一下步骤作图:分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作圆弧,两弧交于点E和点F,作直线EF交AB于点D,连结CD,若AC=8,BC=6,则CD的长为5.
如图,在△ABC中,∠ACB=90°,按一下步骤作图:分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作圆弧,两弧交于点E和点F,作直线EF交AB于点D,连结CD,若AC=8,BC=6,则CD的长为5.
分析 先根据勾股定理求出AB的长,再由作图的方法得出EF是线段AB的垂直平分线,故可得出点D是线段AB的中点,由直角三角形的性质即可得出结论.
解答 解:∵在△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10.
∵由题意可知,EF是线段AB的垂直平分线,
∴点D是线段AB的中点,
∴CD=$\frac{1}{2}$AB=5.
故答案为:5.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2)3=-8a6 | C. | a6÷a2=a3 | D. | ($\frac{1}{2}$)0=0 |
20.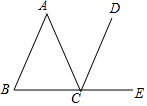 如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
 如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )| A. | 30° | B. | 52.5° | C. | 75° | D. | 85° |
14.摩拜单车进入济南,为市民出行提供了极大方便,摩拜单车来济南第一个月的时间里,1.1万辆车被骑行了3280000人次,3280000用科学记数法表示为( )
| A. | 3.28×102 | B. | 32.8×105 | C. | 3.28×106 | D. | 3.28×107 |
 如图,Rt△OAB的边OA在x轴上,点B在第一象限,点D是斜边OB的中点,反比例函数y=$\frac{k}{x}$经过点D,若S△AOD=6,则k=6.
如图,Rt△OAB的边OA在x轴上,点B在第一象限,点D是斜边OB的中点,反比例函数y=$\frac{k}{x}$经过点D,若S△AOD=6,则k=6. 如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm.
如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm.