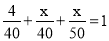��Ŀ����
ij����Ʒÿ���ijɱ���50Ԫ����ij��ʱ��������ÿ��xԪ���ۣ�������(200��2x)���������ʱ�����۳��ù���Ʒ������ΪyԪ��
��1��ֱ��д������y(Ԫ)���ۼ�x(Ԫ)֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ��������������?��������Ƕ��٣�
��3�����Ҫʹ������1200Ԫ���ҳɱ�������2500Ԫ����ֱ��д��x�ķ�ΧΪ_____________��
��1��y=-2x2+300x-10000����2������Ϊ75Ԫʱ���������Ϊ1250Ԫ����3��75��x��80�� �������������������1������������ÿ����������ó�y��x�ĺ�����ϵʽ�� ��2�����ö��κ��������ʽ��н�����⼴�ɣ� ��3������������1200Ԫ���ɱ�������2500Ԫ���в���ʽ�������⼴��. �����������1��������ɵã�y=��x-50����200-2x��=��2x2...
��ϰ��ϵ�д�
 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д� �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
�����Ŀ


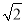 ��
��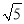 ��
��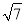 ����3��
����3��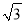 ��3
��3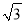 ����4
����4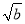 ��
��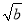 ��3
��3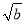 ����3
����3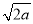 ��
��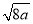 ��
��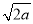 ����
����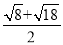 ��
��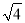 ��
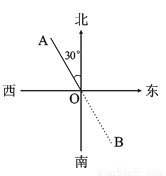
��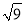 ��2��3��5��������ȷ����( )
��2��3��5��������ȷ����( )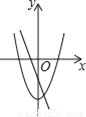 B.
B. 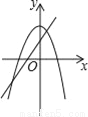 C.
C. 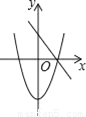 D.
D. 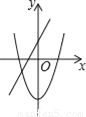
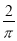 B.
B. 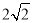 C.
C. 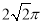 D.
D. 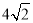
 ��
��
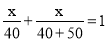 B.
B. 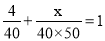 C.
C. 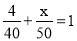 D.
D.