题目内容
抛掷红、蓝两枚六面编号分别为0～5（整数）的质地均匀的正方体骰子将红色和蓝色骰子正面朝上的编号分别作为y=mx+n的一次项系数m和常数项n的值．
（1）问这样可以得到多少个不同形式的一次函数？（只需写出结果）
（2）请求出抛掷红、蓝骰子各一次，得到的一次函数图象与坐标轴围成的面积是
的概率是多少？并说明理由．
（1）问这样可以得到多少个不同形式的一次函数？（只需写出结果）
（2）请求出抛掷红、蓝骰子各一次，得到的一次函数图象与坐标轴围成的面积是
| 25 |
| 2 |
考点：列表法与树状图法,一次函数图象上点的坐标特征
专题：
分析：（1）首先根据题意列出表格，然后由表格即可求得所有等可能的结果．
（2）主要分析说明在上述30种一次函数中，图象与坐标轴围成的三角形中，面积是
是最大的一种，直接利用概率公式求解即可求得答案．
（2）主要分析说明在上述30种一次函数中，图象与坐标轴围成的三角形中，面积是
| 25 |
| 2 |
解答：解：（1）列表得：
∴共可以得到30个不同形式的一次函数；
（2）∵图象与坐标轴围成的三角形中，面积是
是最大的一种（如图），
∴概率为
．
| 5 | （0，5） | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） |
| 4 | （0，4） | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） |
| 3 | （0，3） | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） |
| 2 | （0，2） | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） |
| 1 | （0，1） | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） |
| 0 | （0，0） | （1，0） | （2，0） | （3，0） | （4，0） | （5，0） |
| 0 | 1 | 2 | 3 | 4 | 5 |
（2）∵图象与坐标轴围成的三角形中，面积是| 25 |
| 2 |
∴概率为
| 1 |
| 30 |
点评：本题考查的是用列表法或画树状图法求概率以及一次函数的性质．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如果5x3m-2n-2yn-m+11=0是二元一次方程，则m，n的值为（ ）
| A、3，4 | B、4，3 |
| C、2，2 | D、0，1 |
某数学兴趣小组在探索“圆的有关相交弦问题”时，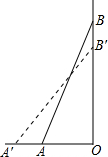
如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为3m，梯子的顶端A向外移动到A′，使梯子的底端A′到墙根O的距离等于4m，同时梯子的顶端B下降至B′，求BB′的长（梯子AB的长为5m）．