题目内容

4．已知：10+$\sqrt{5}$=x+y，其中x是整数，且0＜y＜1，则x-y=14-$\sqrt{5}$．

分析 根据被开方数越大算术平方根越大，可得答案．

解答 解：2$＜\sqrt{5}$＜3，
得12＜10+$\sqrt{5}$＜13，
x=12，y=10+$\sqrt{5}$-12=$\sqrt{5}$-2，
x-y=12-（$\sqrt{5}$-2）=14-$\sqrt{5}$，
故答案为：14-$\sqrt{5}$．

点评 本题考查了实数，利用被开方数越大算术平方根越大得出2$＜\sqrt{5}$＜3是解题关键．

练习册系列答案
相关题目
14．若x2-2x+3=0，则4x2-8x+6=-6．
15．抛物线y=-（x-2）2+1的顶点坐标是（2，1）．
12．下列判断正确的是（　　）
A．3a2bc与bca2不是同类项B．$\frac{{m}^{2}n}{5}$和$\frac{a+b}{2}$都是单项式
C．单项式-x3y2的次数是3，系数是-1D．3x2-y+2xy2是三次三项式
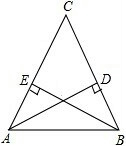19．在等边三角形ABC中，已知点A（-1，-1），且点B，C在函数y=$\frac{1}{x}$（x＞0）的图象上，则△ABC的边长等于2$\sqrt{6}$．
9．如图，从C地看A，B两地的视角∠C是锐角，从C地到A，B两地的距离相等，A地到路段BC的距离AD与B地到路段AC的距离BE相等吗？为什么？
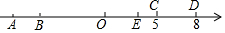16．如图，数轴上有A、B、C、D、O五个点，点O为原点，点C在数轴上表示的数是5，线段CD的长度为3个单位，线段AB的长度为1个单位，且B、C两点之间的距离为12个单位，请解答下列问题：
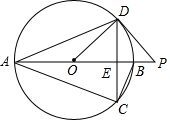（1）点D在数轴上表示的数是8，点A在数轴上表示的数是-8；（2）若点B以每秒2个单位的速度沿数轴向右匀速运动t秒运动到点E处，且CE的长度是2个单位，求点B运动的时间；
（3）把线段CD的中点记作P，如果线段AB以每秒2个单位的速度沿数轴向右匀速运动，同时P点以每秒4个单位的速度沿数轴向左匀速运动，直接写出点P与线段AB的一个端点的距离为1.5个单位时运动的时间．
13．已知：如图，AB是⊙O的直径，CD是弦，且AB⊥CD于E，P是AB延长线上一点，连接PD，∠PDC=∠CAD．
（1）求证：PD是⊙O的切线；
（2）当AB=12，CD=6时，求PD的长．
17．如图，在直角三角形ABC中，两锐角平分线AM、BN所夹的钝角∠AOB=135度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网