题目内容
如图①:点O为直线AB上的点,过点O作射线OC,将一直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在AB的下方.

(1)将图①中三角板绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,问ON所在的直线是否平分∠AOC?并说明理由.
(2)若∠BOC=120°,将图①中的三角板绕点O按每秒5°的速度沿逆时针旋转一周,在旋转过程中,第几秒时直线ON恰好平分∠AOC?

(1)将图①中三角板绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,问ON所在的直线是否平分∠AOC?并说明理由.
(2)若∠BOC=120°,将图①中的三角板绕点O按每秒5°的速度沿逆时针旋转一周,在旋转过程中,第几秒时直线ON恰好平分∠AOC?
考点:角的计算,角平分线的定义
专题:
分析:(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得旋转60°或240°时ON平分∠AOC,据此求解;
(2)由∠BOC=120°可得旋转60°或240°时ON平分∠AOC,据此求解;
解答:解:(1)∵OM平分∠BOC,
∴∠BOM=∠COM,
∵∠MON=90°,
∴∠BOM+∠BON=90°,∠COM+∠COD=90°,
∴∠BON=∠AOD,
∴∠COD=∠AOD,即直线ON平分∠AOC.
(2)ON旋转60°或240°时,ON所在的直线平分∠AOC,用时12秒或48秒.
∴∠BOM=∠COM,
∵∠MON=90°,
∴∠BOM+∠BON=90°,∠COM+∠COD=90°,
∴∠BON=∠AOD,
∴∠COD=∠AOD,即直线ON平分∠AOC.
(2)ON旋转60°或240°时,ON所在的直线平分∠AOC,用时12秒或48秒.
点评:本题主要考查了角平分线的定义及角的计算,认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若关于x的方程2(
-k)x-3x=-1无解,则( )
| 1 |
| 2 |
| A、k=-1 | B、k=l |
| C、k≠-1 | D、k≠1 |
 如图,点D、E分别在△ABC的边BC、AC上,若AB=AC,AD=AE,则( )
如图,点D、E分别在△ABC的边BC、AC上,若AB=AC,AD=AE,则( )| A、当DB为定值时,∠CDE为定值 |
| B、当∠1为定值时,∠CDE为定值 |
| C、当∠2为定值时,∠CDE为定值 |
| D、当∠3为定值时,∠CDE为定值 |
 如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC.
如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC. 已知:如图,在△ABC中,AB=AC,过点A作MN∥BC,点D、E在直线MN上,且DA=EA≠
已知:如图,在△ABC中,AB=AC,过点A作MN∥BC,点D、E在直线MN上,且DA=EA≠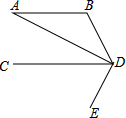 如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数. 如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.
如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.