题目内容
13.计算:(1)($\frac{2}{3}$x-$\frac{3}{2}$y)2;
(2)(2a+b)2+(b-2a)2;
(3)(m+1)(m-1)(m2-1);
(4)(2m+n)2(2m-n)2;
(5)(2x+3)2-(3x+2)2;
(6)(x-y+z)2.
分析 (1)根据完全平方公式计算即可;
(2)根据完全平方公式计算即可;
(3)根据平方差公式和完全平方公式进行计算即可;
(4)根据平方差公式和完全平方公式进行计算即可;
(5)根据平方差公式进行计算即可;
(6)根据完全平方公式进行计算即可.
解答 解:(1)原式=$\frac{4}{9}$x2-2xy+$\frac{9}{4}$y2;
(2)原式=4a2+4ab+b2+4a2-4ab+b2
=8a2+2b2;
(3)原式=(m2-1)(m2-1)
=(m2-1)2
=m4-2m2+1;
(4)原式=[(2m+n)(2m-n)]2
=(4m2-n2)2
=16m4-8m2n2+n4;
(5)原式=[(2x+3)-(3x+2)][(2x+3)+(3x+2)]
=(-x+1)(5x+5);
=-5x2+5;
(6)原式=(x-y)2+2z(x-y)+z2.
=x2-2xy+y2+2xz-2yz+z2.
点评 本题考查了平方差公式和完全平方公式,掌握完全平方公式、平方差公式是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.下列各式-$\frac{1}{2}$mn,m,8,$\frac{1}{a}$,x2+2x+6,$\frac{2x-y}{5}$,$\frac{{x}^{2}+4y}{π}$,$\frac{1}{y}$中,整式有( )
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 7个 |
4.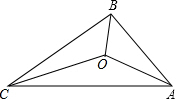 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )| A. | 1:1:1 | B. | 1:2:3 | C. | 2:3:4 | D. | 3:4:5 |
8.下列代数式一定表示正数的是( )
| A. | 2a | B. | a+9 | C. | a2+1 | D. | |a+1| |
18. 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )| A. | 0 | B. | 2 | C. | 4 | D. | 10 |
3.如图正方形中由阴影部分组成的图形,是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |