题目内容
5.已知关于x的方程x2-(2k+1)x+k2+1=0.(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
分析 (1)根据方程解的个数结合根的判别式,即可得出关于k的一元一次不等式,解不等式即可得出结论;
(2)当k=2时,原方程为x2-5x+5=0,设方程的两个为m、n,根据根与系数的关系找出m+n=5、mn=5,将$\sqrt{{m}^{2}+{n}^{2}}$变形为$\sqrt{(m+n)^{2}-2mn}$,再代入数据即可得出结论.
解答 解:(1)∵方程x2-(2k+1)x+k2+1=0有两个不相等的实数根,
∴△=[-(2k+1)]2-4×1×(k2+1)=4k-3>0,
∴k>$\frac{3}{4}$.
(2)当k=2时,原方程为x2-5x+5=0,
设方程的两个为m、n,
∴m+n=5,mn=5,
∴$\sqrt{{m}^{2}+{n}^{2}}$=$\sqrt{(m+n)^{2}-2mn}$=$\sqrt{15}$.
点评 本题考查了根的判别式以及根与系数的关系,熟练掌握当方程有两个不相等的实数根时△>0是解题的关键.

练习册系列答案
相关题目
20.图中不是正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
15.若x=3y,则对x的任何值多项式x2-xy-6y2+3的值( )
| A. | 总是0 | B. | 总是1 | ||
| C. | 随x的取值变化而变化 | D. | 总是3 |
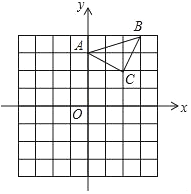 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).