题目内容
抛物线y=x2+ 的开口向__________,对称轴是__________.
的开口向__________,对称轴是__________.
y轴.
【考点】二次函数的性质.
【专题】计算题.
【分析】根据二次函数的性质求解.
【解答】解:抛物线y=x2+ 的开口向
的开口向 上,对称轴为y轴.
上,对称轴为y轴.
故答案为上,y轴.
【点评】本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ,
, ),对称轴直线x=﹣
),对称轴直线x=﹣ ,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣ 时,y随x的增大而减小;x>﹣
时,y随x的增大而减小;x>﹣ 时,y随x的增大而增大;x=﹣
时,y随x的增大而增大;x=﹣ 时,y取得最小值4ac﹣b24a,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣
时,y取得最小值4ac﹣b24a,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣ 时,y随x的增大而增大;x>﹣
时,y随x的增大而增大;x>﹣ 时,y随x的增大而减小;x=﹣
时,y随x的增大而减小;x=﹣ 时,y取得最大值4ac﹣b24a,即顶点是抛物线的最高点.
时,y取得最大值4ac﹣b24a,即顶点是抛物线的最高点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在学习了“25.1.2”概率后,平平和安安两位同学做掷质地均匀的正方体骰子试验,它们共做了120次试验,试验的结果如下表:
| 向上一面的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 18 | 12 | 16 | 40 | 20 |
综合上表,平平说:“如果投掷600次,那么向上一面点数是6的次数正好是100次.”安安说:“一次实验中向上一面点数是5的概率最大”.你认为平平和安安的说法中正确的是( )
A.平平 B.安安 C.都正确 D.都错误
 的算术平方根是( )
的算术平方根是( ) B.
B. C.±
C.±
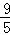 B.
B.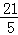 C.
C.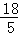 D.
D.